8. 某企业因生产转型,$2$月份产值比$1$月份下降了$20\%$,转型成功后产值呈现良好上升势头,$4$月份比$1$月份增长$15.2\%$.若$3$,$4$,$5$月份的增长率相同,则$5$月份与$1$月份相比增长的百分数约为( )
A. $32\%$
B. $34\%$
C. $36\%$
D. $38\%$
A. $32\%$
B. $34\%$
C. $36\%$
D. $38\%$
答案:
D
9. 如图,点$A$在反比例函数$y=\frac{2}{x}(x\gt0)$的图象上,点$B$在反比例函数$y=\frac{4}{x}(x\gt0)$的图象上,且$AB// x$轴,$BC\perp x$轴于点$C$,则四边形$ABCO$的面积为( )
A. $1$
B. $2$
C. $3$
D. $4$
A. $1$
B. $2$
C. $3$
D. $4$
答案:
C
10. 如图,在菱形$ABCD$中,$E$是边$AD$的中点,连接$BE$,交$AC$于点$F$,连接$DF$.下列四个结论:①$\triangle AEF\backsim\triangle CBF$;②$CF=2AF$;③$DF=DC$;④$2S_{四边形CDEF}=5S_{\triangle ABF}$.其中正确的有( )
A. $4$个
B. $3$个
C. $2$个
D. $1$个
A. $4$个
B. $3$个
C. $2$个
D. $1$个
答案:
B
11. 当$k$______时,方程$(k-5)x^{2}+x=2$是关于$x$的一元二次方程.
答案:
$\neq 5$
12. 如图,$AB// CD$,$AC$与$BD$相交于点$E$.已知$AE=1$,$CE=2$,$DE=3$,则$BD$的长为______.
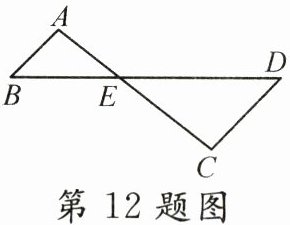

答案:
$\frac{9}{2}$
13. 如图是甲、乙两人$6$次投篮测试(每次投篮$10$个)成绩的统计图,甲、乙两人测试成绩的方差分别记作$s_{甲}^{2}$,$s_{乙}^{2}$,则$s_{甲}^{2}$______$s_{乙}^{2}$.(填“$>$”“$=$”或“$<$”)
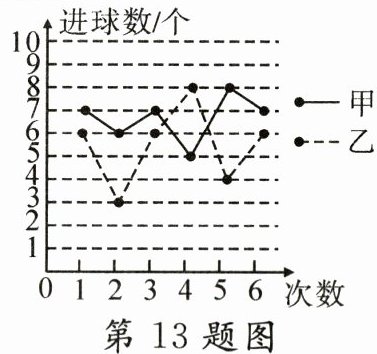

答案:
$<$
14. 在$\triangle ABC$中,$\sin B=\cos(90^{\circ}-\angle C)=\frac{1}{2}$,则$\angle A$的度数是______.
答案:
$120^{\circ}$
15. 如图,在$\square ABCD$中,点$E$在$AB$上,$CE$,$BD$相交于点$F$.若$AE:BE=4:3$,且$BF=2$,则$DF$的长为______.




答案:
$\frac{14}{3}$
16. 小宇每天骑自行车上学,从家到学校所需时间$t(\min)$与骑车速度$v(\text{km}/\text{min})$的关系如图所示.一天早上,由于起床晚了,为了不迟到,需在$15\min$内赶到学校,则他骑车的速度至少是______$\text{km}/\text{min}$.


答案:
0.2
17. 一般地,当$\alpha$,$\beta$为任意角时,$\sin(\alpha+\beta)$与$\sin(\alpha-\beta)$的值可以用下面的公式求得:$\sin(\alpha+\beta)=\sin\alpha\cdot\cos\beta+\cos\alpha\cdot\sin\beta$;$\sin(\alpha-\beta)=\sin\alpha\cdot\cos\beta-\cos\alpha\cdot\sin\beta$.例如,$\sin90^{\circ}=\sin(60^{\circ}+30^{\circ})=\sin60^{\circ}\cdot\cos30^{\circ}+\cos60^{\circ}\cdot\sin30^{\circ}=\frac{\sqrt{3}}{2}\times\frac{\sqrt{3}}{2}+\frac{1}{2}\times\frac{1}{2}=1$.类似地,可以求得$\sin15^{\circ}$的值是______.
答案:
$\frac{\sqrt{6}-\sqrt{2}}{4}$
查看更多完整答案,请扫码查看


