《2025年课时夺冠九年级数学上册湘教版》

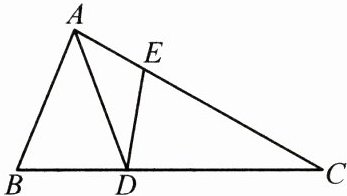
22. （8 分）如图，在 $ \triangle ABC $ 中，点 $ D $ 在 $ BC $ 边上，点 $ E $ 在 $ AC $ 边上，且 $ AD = AB $，$ \angle DEC=\angle ADB $。
（1）求证：$ \triangle AED\sim\triangle ADC $；
（2）若 $ AE = 1 $，$ EC = 3 $，求 $ AB $ 的长。

答案：
(1) 证明：$\because \angle DEC = \angle DAE + \angle ADE$，$\angle ADB = \angle DAE + \angle C$，$\angle DEC = \angle ADB$，$\therefore \angle ADE = \angle C$。$\because \angle DAE = \angle CAD$，$\therefore \triangle AED \sim \triangle ADC$。
(2) 解：$\because AE = 1$，$EC = 3$，$\therefore AC = AE + EC = 4$。由
(1)知 $\triangle AED \sim \triangle ADC$，$\therefore \frac{AD}{AC} = \frac{AE}{AD}$，即 $\frac{AD}{4} = \frac{1}{AD}$，解得 $AD = 2$。$\because AD = AB$，$\therefore AB = 2$。

23. （8 分）如图，一次函数 $ y_{1}=x + 1 $ 的图象与反比例函数 $ y_{2}=\frac{k}{x} $（$ k $ 为常数，且 $ k\neq0 $）的图象都经过点 $ A(m,2) $。
（1）求点 $ A $ 的坐标及反比例函数的表达式；
（2）结合图象直接比较：当 $ x＞0 $ 时，$ y_{1} $ 和 $ y_{2} $ 的大小。

答案： 解：
(1) 把点 $A(m, 2)$ 代入 $y_1 = x + 1$，得 $m + 1 = 2$，解得 $m = 1$，$\therefore$ 点 $A$ 的坐标为 $(1, 2)$。把点 $A(1, 2)$ 代入 $y_2 = \frac{k}{x}$，得 $k = 1 \times 2 = 2$，$\therefore$ 反比例函数的表达式为 $y_2 = \frac{2}{x}$。
(2) 由图象知当 $0 ＜ x ＜ 1$ 时，$y_1 ＜ y_2$；当 $x = 1$ 时，$y_1 = y_2$；当 $x ＞ 1$ 时，$y_1 ＞ y_2$。