18. 如图,点$E$在矩形$ABCD$的边$CD$上,将矩形$ABCD$沿$AE$折叠,点$D$恰好落在边$BC$上的点$F$处.如果$AB:AD = 2:3$,那么$\tan\angle EFC$的值是________.
答案:
$\frac{\sqrt{5}}{2}$
19. (6分)计算:
(1)$\frac{\tan 30^{\circ} + \cos 30^{\circ}}{1 - \cos 60^{\circ}}$;
(2)$\sin 30^{\circ} - 3\tan 30^{\circ} + \tan 60^{\circ} + 2\sin^2 45^{\circ}$.
(1)$\frac{\tan 30^{\circ} + \cos 30^{\circ}}{1 - \cos 60^{\circ}}$;
(2)$\sin 30^{\circ} - 3\tan 30^{\circ} + \tan 60^{\circ} + 2\sin^2 45^{\circ}$.
答案:
解:
(1) 原式 $=\frac{\frac{\sqrt{3}}{3}+\frac{\sqrt{3}}{2}}{1-\frac{1}{2}}=\frac{5\sqrt{3}}{3}$.
(2) 原式 $=\frac{1}{2}-3\times\frac{\sqrt{3}}{3}+\sqrt{3}+2\times(\frac{\sqrt{2}}{2})^{2}=\frac{1}{2}-\sqrt{3}+\sqrt{3}+1=\frac{3}{2}$.
(1) 原式 $=\frac{\frac{\sqrt{3}}{3}+\frac{\sqrt{3}}{2}}{1-\frac{1}{2}}=\frac{5\sqrt{3}}{3}$.
(2) 原式 $=\frac{1}{2}-3\times\frac{\sqrt{3}}{3}+\sqrt{3}+2\times(\frac{\sqrt{2}}{2})^{2}=\frac{1}{2}-\sqrt{3}+\sqrt{3}+1=\frac{3}{2}$.
20. (6分)在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$.
(1)若$\angle A = 30^{\circ}$,$b = \sqrt{3}$,求$\angle B$,$a$,$c$;
(2)若$c = 4$,$b = 2\sqrt{2}$,求$\angle A$,$\angle B$,$a$.
(1)若$\angle A = 30^{\circ}$,$b = \sqrt{3}$,求$\angle B$,$a$,$c$;
(2)若$c = 4$,$b = 2\sqrt{2}$,求$\angle A$,$\angle B$,$a$.
答案:
解:
(1) $\because\angle C=90^{\circ},\angle A=30^{\circ},\therefore\angle B=90^{\circ}-\angle A=60^{\circ}$. 在 $Rt\triangle ABC$ 中, $\sin B=\frac{b}{c}=\frac{\sqrt{3}}{2},\tan A=\frac{a}{b}=\frac{\sqrt{3}}{3}$, 解得 $c=2,a=1$.
(2) 在 $Rt\triangle ABC$ 中, $\sin B=\frac{b}{c}=\frac{2\sqrt{2}}{4}=\frac{\sqrt{2}}{2},\therefore\angle B=45^{\circ},\therefore\angle A=90^{\circ}-\angle B=45^{\circ}.\because\cos B=\frac{a}{c},\therefore a=c\cdot\cos B=4\times\frac{\sqrt{2}}{2}=2\sqrt{2}$.
(1) $\because\angle C=90^{\circ},\angle A=30^{\circ},\therefore\angle B=90^{\circ}-\angle A=60^{\circ}$. 在 $Rt\triangle ABC$ 中, $\sin B=\frac{b}{c}=\frac{\sqrt{3}}{2},\tan A=\frac{a}{b}=\frac{\sqrt{3}}{3}$, 解得 $c=2,a=1$.
(2) 在 $Rt\triangle ABC$ 中, $\sin B=\frac{b}{c}=\frac{2\sqrt{2}}{4}=\frac{\sqrt{2}}{2},\therefore\angle B=45^{\circ},\therefore\angle A=90^{\circ}-\angle B=45^{\circ}.\because\cos B=\frac{a}{c},\therefore a=c\cdot\cos B=4\times\frac{\sqrt{2}}{2}=2\sqrt{2}$.
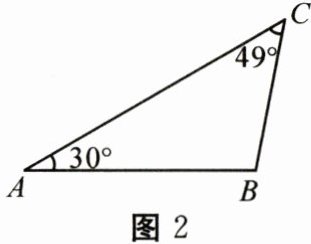
21. (8分)浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图1),某公司的浮式起重机需更换悬索,该公司设计了一个如图2所示的数学模型,测量知$\angle A = 30^{\circ}$,$\angle C = 49^{\circ}$,$AB = 60m$.请你利用以上数据,求出悬索$AC$和支架$BC$的长.(结果精确到1m,参考数据:$\sqrt{3}\approx 1.73$,$\sin 49^{\circ}\approx 0.75$,$\cos 49^{\circ}\approx 0.66$,$\tan 49^{\circ}\approx 1.15$)



答案:
解: 过点 $B$ 作 $BD\perp AC$ 于点 $D,\therefore\angle ADB=90^{\circ}.\because\angle A=30^{\circ},\therefore BD=\frac{1}{2}AB=30m,\therefore AD=\sqrt{AB^{2}-BD^{2}}=30\sqrt{3}m$. 在 $Rt\triangle CBD$ 中, $CD=\frac{BD}{\tan C}\approx26m,BC=\frac{BD}{\sin C}\approx40m,\therefore AC=AD+CD\approx78m$. 答: 悬索 $AC$ 的长约为 $78m$, 支架 $BC$ 的长约为 $40m$.
查看更多完整答案,请扫码查看


