《2025年课时夺冠九年级数学上册湘教版》

1. 下列关于 $ x $ 的方程一定是一元二次方程的是（ ）
A. $ ax^{2}+bx+c = 0 $
B. $ x^{2}+2x=\frac{1}{x} $
C. $ x^{2}-2 = 0 $
D. $ x^{2}+y^{2}=1 $

答案： C

2. 若线段 $ a,b,c,d $ 是成比例线段，且 $ a = 1\mathrm{cm},b = 4\mathrm{cm},c = 2\mathrm{cm} $，则 $ d $ 的长为（ ）
A. $ 8\mathrm{cm} $
B. $ 0.5\mathrm{cm} $
C. $ 2\mathrm{cm} $
D. $ 3\mathrm{cm} $

答案： A

3. 已知变量 $ y $ 与 $ x $ 成反比例，且当 $ x = 3 $ 时，$ y = -6 $，则该反比例函数的表达式为（ ）
A. $ y=\frac{18}{x} $
B. $ y=-\frac{18}{x} $
C. $ y=\frac{2}{x} $
D. $ y=-\frac{2}{x} $

答案： B

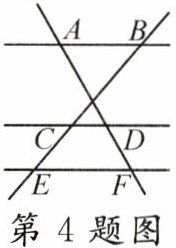
4. 如图，$ AB// CD// EF $，$ AD:DF = 3:1 $，$ BE = 12 $，那么 $ CE $ 的长为（ ）
A. 3
B. 4
C. 5
D. 6

答案： A

5. 对于反比例函数 $ y=\frac{3}{x} $，下列说法正确的是（ ）



A. 图象经过点 $ (1,-3) $
B. 图象在第二、四象限
C. 当 $ x＞0 $ 时，$ y $ 随 $ x $ 的增大而增大
D. 当 $ x＜0 $ 时，$ y $ 随 $ x $ 的增大而减小

答案： D

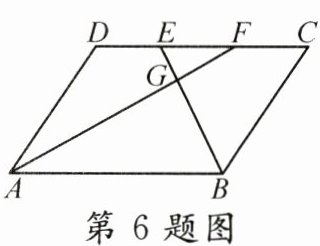
6. 如图，四边形 $ ABCD $ 为平行四边形，$ E,F $ 为边 $ CD $ 的三等分点，连接 $ AF,BE $，相交于点 $ G $，则 $ S_{\triangle EFG}:S_{\triangle ABG} $ 等于（ ）
A. $ 1:3 $
B. $ 3:1 $
C. $ 1:9 $
D. $ 9:1 $

答案： C

7. 若关于 $ x $ 的一元二次方程 $ (k - 1)x^{2}+2x - 2 = 0 $ 有两个不相等的实数根，则 $ k $ 的取值范围为（ ）
A. $ k＞\frac{1}{2} $ 且 $ k\neq1 $
B. $ k＞\frac{1}{2} $
C. $ k\geqslant\frac{1}{2} $ 且 $ k\neq1 $
D. $ k\geqslant\frac{1}{2} $

答案： A

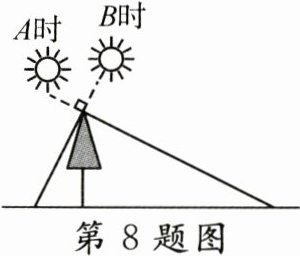
8. 如图，小明在 $ A $ 时测得某树的影长为 $ 8\mathrm{m} $，$ B $ 时又测得该树的影长为 $ 2\mathrm{m} $。若两次日照的光线互相垂直，则树的高度为（ ）
A. $ 2\mathrm{m} $
B. $ 4\mathrm{m} $
C. $ 6\mathrm{m} $
D. $ 8\mathrm{m} $

答案： B