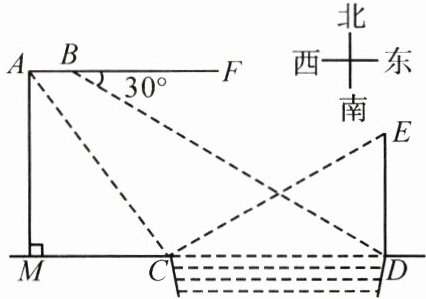
26. (12分)某校数学兴趣小组在水库某段$CD$的附近借助无人机进行实物测量的社会实践活动.如图,兴趣小组在水库正面左岸的$C$处测得水库右岸$D$处某标志物$DE$顶端的仰角为$\alpha$.在$C$处一架无人飞机沿北偏西$(90^{\circ} - \beta)$方向飞行$100\sqrt{5}m$到达$A$处,无人机沿水平线$AF$方向继续飞行30m至$B$处,测得正前方水库右岸$D$处的俯角为$30^{\circ}$.线段$AM$的长为无人机距地面的铅直高度,点$M$,$C$,$D$在同一条直线上.
(1)求无人机的飞行高度$AM$;
(2)求标志物$DE$的高度.(结果精确到0.1m,参考数据:$\sin\alpha = \frac{3}{5}$,$\cos\alpha = \frac{4}{5}$,$\tan\alpha = \frac{3}{4}$,$\sin\beta = \frac{2\sqrt{5}}{5}$,$\cos\beta = \frac{\sqrt{5}}{5}$,$\tan\beta = 2$,$\sqrt{3}\approx 1.732$)
(1)求无人机的飞行高度$AM$;
(2)求标志物$DE$的高度.(结果精确到0.1m,参考数据:$\sin\alpha = \frac{3}{5}$,$\cos\alpha = \frac{4}{5}$,$\tan\alpha = \frac{3}{4}$,$\sin\beta = \frac{2\sqrt{5}}{5}$,$\cos\beta = \frac{\sqrt{5}}{5}$,$\tan\beta = 2$,$\sqrt{3}\approx 1.732$)

答案:
解:
(1) 根据题意可知 $\angle ACM=\beta,AC=100\sqrt{5}m$. 在 $Rt\triangle AMC$ 中, $\sin\angle ACM=\frac{AM}{AC},\therefore AM=AC\cdot\sin\beta=100\sqrt{5}\times\frac{2\sqrt{5}}{5}=200(m)$. 答: 无人机的飞行高度 $AM$ 为 $200m$.
(2) 根据题意可知 $\angle ECD=\alpha,AB=30m,\angle FBD=30^{\circ}$. 由
(1) 知 $AM=200m$. 过点 $B$ 作 $BG\perp MC$ 于点 $G$, 交 $AC$ 于点 $H,\therefore$ 四边形 $ABGM$ 是矩形, $\therefore\angle ABH=90^{\circ},BG=AM=200m$. 根据题意可知 $AB// CM,\therefore\angle BAH=\angle ACM=\beta,\angle BDG=\angle FBD=30^{\circ}$. 在 $Rt\triangle ABH$ 中, $\tan\angle BAH=\frac{BH}{AB},\therefore BH=AB\cdot\tan\beta=30\times2=60(m),\therefore HG=BG-BH=200-60=140(m)$. 在 $Rt\triangle CHG$ 中, $\tan\angle HCG=\frac{HG}{CG},\therefore CG=\frac{HG}{\tan\beta}=\frac{140}{2}=70(m)$. 在 $Rt\triangle BGD$ 中, $\tan\angle BDG=\frac{BG}{GD},\therefore GD=\frac{BG}{\tan\angle BDG}=200\sqrt{3}m,\therefore CD=GD-GC=(200\sqrt{3}-70)m$. 在 $Rt\triangle ECD$ 中, $\tan\angle ECD=\frac{DE}{CD},\therefore DE=CD\cdot\tan\alpha=(200\sqrt{3}-70)\times\frac{3}{4}\approx207.3(m)$. 答: 标志物 $DE$ 的高度约为 $207.3m$.
(1) 根据题意可知 $\angle ACM=\beta,AC=100\sqrt{5}m$. 在 $Rt\triangle AMC$ 中, $\sin\angle ACM=\frac{AM}{AC},\therefore AM=AC\cdot\sin\beta=100\sqrt{5}\times\frac{2\sqrt{5}}{5}=200(m)$. 答: 无人机的飞行高度 $AM$ 为 $200m$.
(2) 根据题意可知 $\angle ECD=\alpha,AB=30m,\angle FBD=30^{\circ}$. 由
(1) 知 $AM=200m$. 过点 $B$ 作 $BG\perp MC$ 于点 $G$, 交 $AC$ 于点 $H,\therefore$ 四边形 $ABGM$ 是矩形, $\therefore\angle ABH=90^{\circ},BG=AM=200m$. 根据题意可知 $AB// CM,\therefore\angle BAH=\angle ACM=\beta,\angle BDG=\angle FBD=30^{\circ}$. 在 $Rt\triangle ABH$ 中, $\tan\angle BAH=\frac{BH}{AB},\therefore BH=AB\cdot\tan\beta=30\times2=60(m),\therefore HG=BG-BH=200-60=140(m)$. 在 $Rt\triangle CHG$ 中, $\tan\angle HCG=\frac{HG}{CG},\therefore CG=\frac{HG}{\tan\beta}=\frac{140}{2}=70(m)$. 在 $Rt\triangle BGD$ 中, $\tan\angle BDG=\frac{BG}{GD},\therefore GD=\frac{BG}{\tan\angle BDG}=200\sqrt{3}m,\therefore CD=GD-GC=(200\sqrt{3}-70)m$. 在 $Rt\triangle ECD$ 中, $\tan\angle ECD=\frac{DE}{CD},\therefore DE=CD\cdot\tan\alpha=(200\sqrt{3}-70)\times\frac{3}{4}\approx207.3(m)$. 答: 标志物 $DE$ 的高度约为 $207.3m$.
查看更多完整答案,请扫码查看


