23. (8分)如图,在$\triangle ABC$中,点$D$在边$BC$上,$\angle ADE=\angle ABC$,$\angle EAF=\angle FDC$,$DE$与$AC$相交于点$F$.
(1)求证:$\frac{AB}{AC}=\frac{AD}{AE}$;
(2)连接$BF$,若$AB^2 = AF\cdot AC$,求证:$AD\cdot BC = AE\cdot BF$.
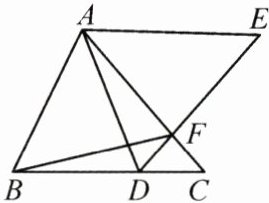
(1)求证:$\frac{AB}{AC}=\frac{AD}{AE}$;
(2)连接$BF$,若$AB^2 = AF\cdot AC$,求证:$AD\cdot BC = AE\cdot BF$.

答案:
证明:(1)$ \because \angle E A F + \angle A F E + \angle E = \angle F D C + \angle C F D + \angle C = 180 ^ { \circ } $,$ \angle E A F = \angle F D C $,$ \angle A F E = \angle C F D $,$ \therefore \angle E = \angle C $。$ \because \angle A D E = \angle A B C $,$ \therefore \triangle A D E \backsim \triangle A B C $,$ \therefore \frac { A E } { A C } = \frac { A D } { A B } $,即 $ \frac { A B } { A C } = \frac { A D } { A E } $。(2)$ \because A B ^ { 2 } = A F \cdot A C $,$ \therefore \frac { A B } { A C } = \frac { A F } { A B } $。$ \because \angle B A C = \angle F A B $,$ \therefore \triangle A B C \backsim \triangle A F B $,$ \therefore \frac { A B } { A F } = \frac { B C } { B F } $,$ \therefore \frac { A F } { A B } = \frac { B F } { B C } $,$ \therefore \frac { A B } { A C } = \frac { B F } { B C } $。由(1)知 $ \frac { A B } { A C } = \frac { A D } { A E } $,$ \therefore \frac { B F } { B C } = \frac { A D } { A E } $,$ \therefore A D \cdot B C = A E \cdot B F $。
24. (8分)如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点$G$处,手电筒的光从平面镜上点$B$处反射后,恰好经过木板的边缘点$F$,落在墙上的点$E$处,测得点$E$到地面的高度$DE = 3.5m$,点$F$到地面的高度$CF = 1.5m$,灯泡到木板的水平距离$AC = 5.4m$,墙到木板的水平距离为$CD = 4m$.已知光在镜面反射中的入射角等于反射角,图中点$A$,$B$,$C$,$D$在同一水平面上.
(1)求$BC$的长;
(2)求灯泡到地面的高度$AG$.
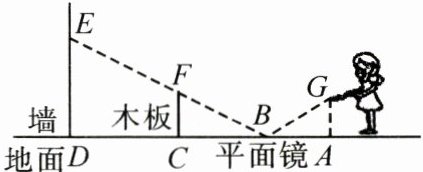
(1)求$BC$的长;
(2)求灯泡到地面的高度$AG$.

答案:
解:(1)由题意,得 $ C F // D E $,$ \therefore \triangle B C F \backsim \triangle B D E $,$ \therefore \frac { B C } { B D } = \frac { C F } { D E } $,即 $ \frac { B C } { B C + 4 } = \frac { 1.5 } { 3.5 } $,$ \therefore B C = 3 \mathrm { m } $。(2)由(1)知 $ B C = 3 \mathrm { m } $,$ \therefore A B = A C - B C = 2.4 \mathrm { m } $。$ \because $ 光在镜面反射中的入射角等于反射角,$ \therefore \angle G B A = \angle F B C $。由题意,得 $ \angle G A B = \angle F C B = 90 ^ { \circ } $,$ \therefore \triangle B A G \backsim \triangle B C F $,$ \therefore \frac { A G } { C F } = \frac { A B } { B C } $,即 $ \frac { A G } { 1.5 } = \frac { 2.4 } { 3 } $,$ \therefore A G = 1.2 \mathrm { m } $。答:灯泡到地面的高度 $ A G $ 为 $ 1.2 \mathrm { m } $。
查看更多完整答案,请扫码查看


