《2025年课时夺冠九年级数学上册湘教版》

21. （8分）如图，在平行四边形$ABCD$中，$E$为边$DC$上一点，$\angle EAB=\angle CBE$．
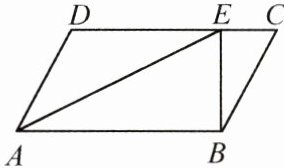
（1）求证：$\triangle ABE\backsim\triangle BEC$；
（2）若$AB = 4$，$DE = 3$，求$BE$的长．

答案： （1）证明：$ \because $ 四边形 $ A B C D $ 是平行四边形，$ \therefore A B // C D $，$ \therefore \angle E B A = \angle C E B $。$ \because \angle E A B = \angle C B E $，$ \therefore \triangle A B E \backsim \triangle B E C $。（2）解：$ \because $ 四边形 $ A B C D $ 是平行四边形，$ \therefore D C = A B = 4 $，$ \therefore E C = D C - D E = 4 - 3 = 1 $。由（1）知 $ \triangle A B E \backsim \triangle B E C $，$ \therefore \frac { A B } { B E } = \frac { B E } { E C } $，$ \therefore B E ^ { 2 } = A B \cdot E C = 4 \times 1 = 4 $，$ \therefore B E = 2 $。

22. （8分）如图，在平面直角坐标系中，$\triangle ABC$的三个顶点的坐标分别为$A(-2,1)$，$B(-1,4)$，$C(-3,2)$．
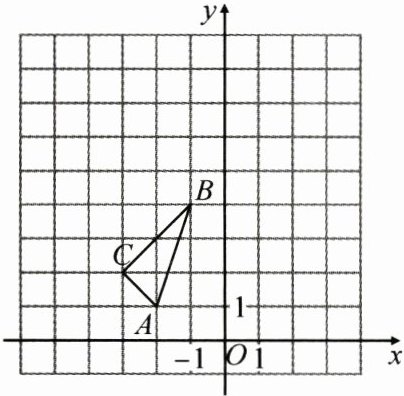
（1）以原点$O$为位似中心，将$\triangle ABC$放大为原图形的$2$倍，在$y$轴的左侧画出所得到的$\triangle A_1B_1C_1$，并写出点$C_1$的坐标；
（2）如果点$D(a,b)$在线段$AB$上，请直接写出经过（1）中的变化后点$D$的对应点$D_1$的坐标．

答案： 解：（1）图略，点 $ C _ { 1 } $ 的坐标为 $ ( - 6,4 ) $。（2）点 $ D _ { 1 } $ 的坐标为 $ ( 2 a, 2 b ) $。