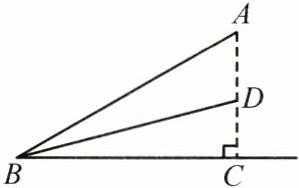
22. (8分)如图,学校校园内有一小山坡$AB$,经测量,坡角$\angle ABC = 30^{\circ}$,斜坡$AB$长为12m.为方便学生行走,决定开挖小山坡,使斜坡$BD$的坡度为$1:3$.$A$,$D$两点处于同一铅垂线上,求挖完后小山坡下降的高度$AD$.(结果保留根号)

答案:
解: 在 $Rt\triangle ABC$ 中, $\angle ABC=30^{\circ},\therefore AC=AB\cdot\sin\angle ABC=12\times\frac{1}{2}=6(m),BC=AB\cdot\cos\angle ABC=12\times\frac{\sqrt{3}}{2}=6\sqrt{3}(m).\because$ 斜坡 $BD$ 的坡度是 $1:3,\therefore CD=\frac{1}{3}BC=2\sqrt{3}m,\therefore AD=AC-CD=(6-2\sqrt{3})m$. 答: 挖完后小山坡下降的高度 $AD$ 为 $(6-2\sqrt{3})m$.
23. (8分)如图,在$\triangle ABC$中,$AD$与$CE$分别是边$BC$与$AB$上的高.已知$AB = 12$,$BC = 16$,$S_{\triangle ABC} = 48$.
(1)求$\angle B$的度数;
(2)求$\tan\angle ACB$的值.

(1)求$\angle B$的度数;
(2)求$\tan\angle ACB$的值.

答案:
解:
(1) 由题意可知 $S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}\times16\times AD=48$, 解得 $AD=6,\therefore$ 在 $Rt\triangle ABD$ 中, $\sin B=\frac{AD}{AB}=\frac{1}{2},\therefore\angle B=30^{\circ}$.
(2) 由
(1) 知 $AD=6$. 在 $Rt\triangle ABD$ 中, $BD=\sqrt{AB^{2}-AD^{2}}=6\sqrt{3},\therefore CD=BC-BD=16-6\sqrt{3}$. 在 $Rt\triangle ACD$ 中, $\tan\angle ACB=\frac{AD}{CD}=\frac{6}{16-6\sqrt{3}}=\frac{24+9\sqrt{3}}{37}$.
(1) 由题意可知 $S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}\times16\times AD=48$, 解得 $AD=6,\therefore$ 在 $Rt\triangle ABD$ 中, $\sin B=\frac{AD}{AB}=\frac{1}{2},\therefore\angle B=30^{\circ}$.
(2) 由
(1) 知 $AD=6$. 在 $Rt\triangle ABD$ 中, $BD=\sqrt{AB^{2}-AD^{2}}=6\sqrt{3},\therefore CD=BC-BD=16-6\sqrt{3}$. 在 $Rt\triangle ACD$ 中, $\tan\angle ACB=\frac{AD}{CD}=\frac{6}{16-6\sqrt{3}}=\frac{24+9\sqrt{3}}{37}$.
查看更多完整答案,请扫码查看


