《2025年课时夺冠九年级数学上册湘教版》

24. （8 分）已知关于 $ x $ 的一元二次方程 $ kx^{2}+(k + 1)x+\frac{k}{4}=0 $ 有实数根。
（1）求 $ k $ 的取值范围；
（2）是否存在实数 $ k $，使方程有两个不相等的实数根且它们的倒数和为 0？若存在，求出 $ k $ 的值；若不存在，请说明理由。

答案： 解：
(1) 由题意，得 $\Delta = (k + 1)^2 - 4k \cdot \frac{k}{4} = 2k + 1 \geq 0$，且 $k \neq 0$，解得 $k \geq -\frac{1}{2}$ 且 $k \neq 0$。
(2) 不存在。理由如下：设方程的两根分别是 $x_1$ 和 $x_2$。由根与系数的关系，得 $x_1 + x_2 = -\frac{k + 1}{k}$，$x_1x_2 = \frac{1}{4}$。$\because \frac{1}{x_1} + \frac{1}{x_2} = \frac{x_1 + x_2}{x_1x_2} = 0$，$\therefore \frac{-\frac{k + 1}{k}}{\frac{1}{4}} = 0$，即 $-\frac{4(k + 1)}{k} = 0$，解得 $k = -1$。经检验，$k = -1$ 是分式方程的解。由
(1)知 $k \geq -\frac{1}{2}$，$\therefore k = -1$ 不符合题意，舍去，$\therefore$ 不存在实数 $k$，使方程有两个不相等的实数根，且它们的倒数和为 0。

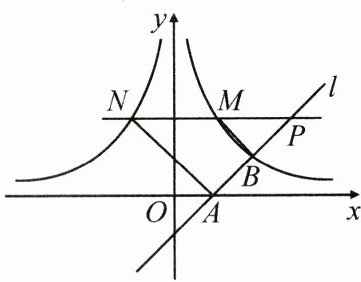
25. （10 分）如图，经过点 $ A(1,0) $ 的直线 $ l $ 与双曲线 $ y=\frac{m}{x}(x＞0) $ 交于点 $ B(2,1) $，直线 $ y = 2 $ 分别交双曲线 $ y=\frac{m}{x}(x＞0) $ 和 $ y=-\frac{m}{x}(x＜0) $ 于点 $ M,N $，交直线 $ l $ 于点 $ P(p,p - 1)(p＞1) $，连接 $ BM,AN $。
（1）求 $ m $ 的值及直线 $ l $ 的表达式；
（2）求证：$ BM// AN $。

答案：
(1) 解：把点 $B(2, 1)$ 代入 $y = \frac{m}{x}$，得 $m = 2$。设直线 $l$ 的表达式是 $y = kx + b(k \neq 0)$。把点 $A$，$B$ 的坐标代入，得 $\begin{cases} k + b = 0, \\ 2k + b = 1, \end{cases}$ 解得 $\begin{cases} k = 1, \\ b = -1, \end{cases}$ $\therefore$ 直线 $l$ 的表达式是 $y = x - 1$。
(2) 证明：$\because$ 点 $P(p, p - 1)$ 在直线 $y = 2$ 上，$\therefore p - 1 = 2$，解得 $p = 3$，$\therefore$ 点 $P$ 的坐标是 $(3, 2)$。把 $y = 2$ 代入 $y = \frac{2}{x}$，得 $x = 1$，$\therefore$ 点 $M$ 的坐标是 $(1, 2)$，$\therefore PM = 3 - 1 = 2$。把 $y = 2$ 代入 $y = -\frac{2}{x}$，得 $x = -1$，$\therefore$ 点 $N$ 的坐标是 $(-1, 2)$，$\therefore PN = 3 - (-1) = 4$。$\because$ 点 $P$，$A$，$B$ 的坐标分别为 $P(3, 2)$，$A(1, 0)$，$B(2, 1)$，$\therefore PB = \sqrt{(3 - 2)^2 + (2 - 1)^2} = \sqrt{2}$，$PA = \sqrt{(3 - 1)^2 + (2 - 0)^2} = 2\sqrt{2}$，$\therefore \frac{PM}{PN} = \frac{PB}{PA} = \frac{1}{2}$。$\because \angle MPB = \angle NPA$，$\therefore \triangle MPB \sim \triangle NPA$，$\therefore \angle PMB = \angle PNA$，$\therefore BM // AN$。