18. 如图,点$E$,$F$均在反比例函数$y=\frac{2}{x}$的图象上,直线$EF$分别与$x$轴、$y$轴交于点$A$,$B$,且$BE:BF=1:3$,则$\triangle EOF$的面积是______.
答案:
$\frac{8}{3}$
19. (6分)解下列方程:
(1)$(x-2)^{2}=16$; (2)$x^{2}-3x+1=0$.
(1)$(x-2)^{2}=16$; (2)$x^{2}-3x+1=0$.
答案:
解:
(1)根据平方根的意义, 得 $x - 2 = 4$ 或 $x - 2 = - 4$. 因此, 原方程的根为 $x_{1} = 6$, $x_{2} = - 2$.
(2) 这里 $a = 1$, $b = - 3$, $c = 1$. 因而 $b^{2} - 4ac = (- 3)^{2} - 4 \times 1 = 5 > 0$, $\therefore x = \frac{3 \pm \sqrt{5}}{2}$. 因此, 原方程的根为 $x_{1} = \frac{3 + \sqrt{5}}{2}$, $x_{2} = \frac{3 - \sqrt{5}}{2}$.
(1)根据平方根的意义, 得 $x - 2 = 4$ 或 $x - 2 = - 4$. 因此, 原方程的根为 $x_{1} = 6$, $x_{2} = - 2$.
(2) 这里 $a = 1$, $b = - 3$, $c = 1$. 因而 $b^{2} - 4ac = (- 3)^{2} - 4 \times 1 = 5 > 0$, $\therefore x = \frac{3 \pm \sqrt{5}}{2}$. 因此, 原方程的根为 $x_{1} = \frac{3 + \sqrt{5}}{2}$, $x_{2} = \frac{3 - \sqrt{5}}{2}$.
20. (6分)如图,在平面直角坐标系中,$\triangle ABC$的顶点均在格点(网格线的交点)上,已知点$A(1,0)$,$B(2,4)$,$C(4,1)$.
(1)以点$O$为位似中心,在第一象限内画出$\triangle ABC$的位似图形$\triangle A^{\prime}B^{\prime}C^{\prime}$,使$\triangle A^{\prime}B^{\prime}C^{\prime}$与$\triangle ABC$的位似比为$2:1$;
(2)写出点$B^{\prime}$,$C^{\prime}$的坐标.

(1)以点$O$为位似中心,在第一象限内画出$\triangle ABC$的位似图形$\triangle A^{\prime}B^{\prime}C^{\prime}$,使$\triangle A^{\prime}B^{\prime}C^{\prime}$与$\triangle ABC$的位似比为$2:1$;
(2)写出点$B^{\prime}$,$C^{\prime}$的坐标.

答案:
解:
(1) 略.
(2) 点 $B'(4,8)$, 点 $C'(8,2)$.
(1) 略.
(2) 点 $B'(4,8)$, 点 $C'(8,2)$.
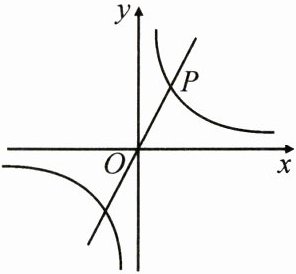
21. (8分)如图,正比例函数$y_{1}=2x$的图象与反比例函数$y_{2}=\frac{k}{x}$的图象有一个交点为$P(2,m)$.
(1)求反比例函数$y_{2}=\frac{k}{x}$的表达式;
(2)根据图象,直接写出当$y_{1}\gt y_{2}$时,$x$的取值范围.
(1)求反比例函数$y_{2}=\frac{k}{x}$的表达式;
(2)根据图象,直接写出当$y_{1}\gt y_{2}$时,$x$的取值范围.

答案:
解:
(1) 将点 $P(2,m)$ 代人 $y_{1} = 2x$, 得 $m = 4$, $\therefore$ 点 $P$ 的坐标为 $(2,4)$. 将点 $P(2,4)$ 代人 $y_{2} = \frac{k}{x}$, 得 $k = 2 \times 4 = 8$, $\therefore$ 反比例函数的表达式为 $y_{2} = \frac{8}{x}$.
(2) 由图象知, 当 $y_{1} > y_{2}$ 时, $x$ 的取值范围为 $- 2 < x < 0$ 或 $x > 2$.
(1) 将点 $P(2,m)$ 代人 $y_{1} = 2x$, 得 $m = 4$, $\therefore$ 点 $P$ 的坐标为 $(2,4)$. 将点 $P(2,4)$ 代人 $y_{2} = \frac{k}{x}$, 得 $k = 2 \times 4 = 8$, $\therefore$ 反比例函数的表达式为 $y_{2} = \frac{8}{x}$.
(2) 由图象知, 当 $y_{1} > y_{2}$ 时, $x$ 的取值范围为 $- 2 < x < 0$ 或 $x > 2$.
查看更多完整答案,请扫码查看


