24. (8分)如图,反比例函数 $ y = \frac { m } { x } $ 的图象与一次函数 $ y = k x + b $ 的图象相交于点 $ A ( 2, 6 ) $,$ B ( n, 1 ) $.
(1)求反比例函数与一次函数的表达式;
(2)直线 $ A B $ 与 $ y $ 轴交于点 $ P $,$ E $ 为 $ y $ 轴上的一个动点,连接 $ A E $,$ B E $. 若 $ S _ { \triangle A E B } = 5 $,求点 $ E $ 的坐标.

(1)求反比例函数与一次函数的表达式;
(2)直线 $ A B $ 与 $ y $ 轴交于点 $ P $,$ E $ 为 $ y $ 轴上的一个动点,连接 $ A E $,$ B E $. 若 $ S _ { \triangle A E B } = 5 $,求点 $ E $ 的坐标.

答案:
解:
(1) 将点 $A(2,6)$ 代入 $y=\frac{m}{x}$,得 $m=12$,$\therefore$ 反比例函数的表达式为 $y=\frac{12}{x}$。将点 $B(n, 1)$ 代入 $y=\frac{12}{x}$,得 $n=12$,$\therefore$ 点 $B$ 的坐标为 $(12,1)$。将点 $A(2,6), B(12,1)$ 代入 $y=k x+b$,得 $\left\{\begin{array}{l}2 k+b=6, \\ 12 k+b=1,\end{array}\right.$ 解得 $\left\{\begin{array}{l}k=-\frac{1}{2}, \\ b=7,\end{array}\right.$ $\therefore$ 一次函数的表达式为 $y=-\frac{1}{2} x+7$。
(2) 设点 $E$ 的坐标为 $(0, t)$。在 $y=-\frac{1}{2} x+7$ 中,当 $x=0$ 时,$y=7$,$\therefore$ 点 $P$ 的坐标为 $(0,7)$,$\therefore P E=|t-7|$。$\because S_{\triangle A E B}=S_{\triangle B E P}-S_{\triangle A E P}=5$,$\therefore \frac{1}{2} \times|t-7| \times(12-2)=5$,$\therefore|t-7|=1$,解得 $t=6$ 或 $t=8$,$\therefore$ 点 $E$ 的坐标为 $(0,6)$ 或 $(0,8)$。
(1) 将点 $A(2,6)$ 代入 $y=\frac{m}{x}$,得 $m=12$,$\therefore$ 反比例函数的表达式为 $y=\frac{12}{x}$。将点 $B(n, 1)$ 代入 $y=\frac{12}{x}$,得 $n=12$,$\therefore$ 点 $B$ 的坐标为 $(12,1)$。将点 $A(2,6), B(12,1)$ 代入 $y=k x+b$,得 $\left\{\begin{array}{l}2 k+b=6, \\ 12 k+b=1,\end{array}\right.$ 解得 $\left\{\begin{array}{l}k=-\frac{1}{2}, \\ b=7,\end{array}\right.$ $\therefore$ 一次函数的表达式为 $y=-\frac{1}{2} x+7$。
(2) 设点 $E$ 的坐标为 $(0, t)$。在 $y=-\frac{1}{2} x+7$ 中,当 $x=0$ 时,$y=7$,$\therefore$ 点 $P$ 的坐标为 $(0,7)$,$\therefore P E=|t-7|$。$\because S_{\triangle A E B}=S_{\triangle B E P}-S_{\triangle A E P}=5$,$\therefore \frac{1}{2} \times|t-7| \times(12-2)=5$,$\therefore|t-7|=1$,解得 $t=6$ 或 $t=8$,$\therefore$ 点 $E$ 的坐标为 $(0,6)$ 或 $(0,8)$。
25. (10分)【背景】点 $ A $ 在反比例函数 $ y = \frac { k } { x } ( k > 0 ) $ 的图象上. $ A B \perp x $ 轴于点 $ B $,$ A C \perp y $ 轴于点 $ C $,分别在射线 $ A C $,$ B O $ 上取点 $ D $,$ E $,使得四边形 $ A B E D $ 为正方形,如图1,点 $ A $ 在第一象限内,当 $ A C = 4 $ 时,小李测得 $ C D = 3.5 $.
【探究】通过改变点 $ A $ 的位置,小李发现点 $ D $,$ A $ 的横坐标之间存在函数关系. 请帮助小李解答下列问题:
(1)求 $ k $ 的值;
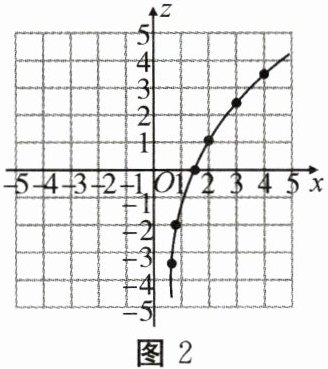
(2)设点 $ A $,$ D $ 的横坐标分别为 $ x $,$ z $,将 $ z $ 关于 $ x $ 的函数称为“$ Z $ 函数”,如图2,小李画出了 $ x > 0 $ 时“$ Z $ 函数”的图象.
①求这个“$ Z $ 函数”的表达式;
②补画 $ x < 0 $ 时“$ Z $ 函数”的图象,并写出这个函数的性质.(两条即可)

【探究】通过改变点 $ A $ 的位置,小李发现点 $ D $,$ A $ 的横坐标之间存在函数关系. 请帮助小李解答下列问题:
(1)求 $ k $ 的值;
(2)设点 $ A $,$ D $ 的横坐标分别为 $ x $,$ z $,将 $ z $ 关于 $ x $ 的函数称为“$ Z $ 函数”,如图2,小李画出了 $ x > 0 $ 时“$ Z $ 函数”的图象.
①求这个“$ Z $ 函数”的表达式;
②补画 $ x < 0 $ 时“$ Z $ 函数”的图象,并写出这个函数的性质.(两条即可)


答案:
解:
(1) 当 $AC=4, CD=3.5$ 时,$AD=0.5$。$\because$ 四边形 $ABED$ 是正方形,$\therefore AB=AD=0.5$,$\therefore A(4,0.5)$。$\because$ 点 $A$ 在反比例函数 $y=\frac{k}{x}(k>0)$ 的图象上,$\therefore k=4 \times 0.5=2$。
(2) ① 由题意知点 $A$ 的坐标为 $(x, x-z)$,$\therefore x(x-z)=2$,$\therefore z=x-\frac{2}{x}$。② 图略。性质:当 $x>0$ 时,$z$ 随 $x$ 的增大而增大;当 $x<0$ 时,$z$ 随 $x$ 的增大而增大。函数图象与 $z$ 轴无交点。(答案不唯一)
(1) 当 $AC=4, CD=3.5$ 时,$AD=0.5$。$\because$ 四边形 $ABED$ 是正方形,$\therefore AB=AD=0.5$,$\therefore A(4,0.5)$。$\because$ 点 $A$ 在反比例函数 $y=\frac{k}{x}(k>0)$ 的图象上,$\therefore k=4 \times 0.5=2$。
(2) ① 由题意知点 $A$ 的坐标为 $(x, x-z)$,$\therefore x(x-z)=2$,$\therefore z=x-\frac{2}{x}$。② 图略。性质:当 $x>0$ 时,$z$ 随 $x$ 的增大而增大;当 $x<0$ 时,$z$ 随 $x$ 的增大而增大。函数图象与 $z$ 轴无交点。(答案不唯一)
查看更多完整答案,请扫码查看


