《2025年课时夺冠九年级数学上册湘教版》

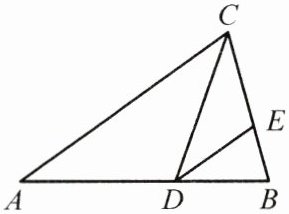
25. （10分）如图，在$\triangle ABC$中，$CD$是角平分线，$DE$平分$\angle CDB$，交$BC$于点$E$，且$DE// AC$．
（1）求证：$CD^2 = CA\cdot CE$；
（2）若$CE = 2BE = 2$，求$CD$的长．

答案： （1）证明：$ \because C D $ 是角平分线，$ \therefore \angle A C D = \angle D C E $。$ \because D E $ 平分 $ \angle C D B $，$ \therefore \angle C D E = \angle E D B $。$ \because D E // A C $，$ \therefore \angle A = \angle E D B $，$ \therefore \angle A = \angle C D E $，$ \therefore \triangle A C D \backsim \triangle D C E $，$ \therefore \frac { C A } { C D } = \frac { C D } { C E } $，$ \therefore C D ^ { 2 } = C A \cdot C E $。（2）解：$ \because C E = 2 B E = 2 $，$ \therefore B E = 1 $，$ \therefore B C = B E + C E = 3 $。由（1）知 $ \angle A C D = \angle B C D $。$ \because D E // A C $，$ \therefore \angle A C D = \angle C D E $，$ \therefore \angle B C D = \angle C D E $，$ \therefore D E = C E = 2 $。$ \because D E // A C $，$ \therefore \triangle B D E \backsim \triangle B A C $，$ \therefore \frac { D E } { A C } = \frac { B E } { B C } = \frac { 1 } { 3 } $，$ \therefore C A = 3 D E = 6 $。由（1）知 $ C D ^ { 2 } = C A \cdot C E $，$ \therefore C D ^ { 2 } = 6 \times 2 = 12 $，$ \therefore C D = 2 \sqrt { 3 } $。

26. （12分）在$\triangle ABC$中，$\angle ACB = 90^{\circ}$，$BE$是边$AC$上的中线，点$D$在射线$BC$上．
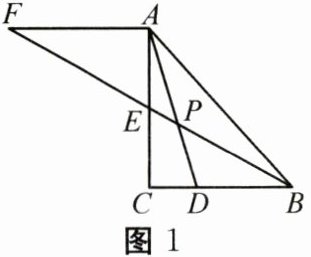
【猜想】如图1，若点$D$在边$BC$上，$BD:BC = 2:3$，$AD$与$BE$相交于点$P$，过点$A$作$AF// BC$，交$BE$的延长线于点$F$，则$\frac{AP}{DP}$的值为________；
【探究】如图2，若点$D$在$BC$的延长线上，$AD$与$BE$的延长线交于点$P$，$CD:BC = 1:2$，求$\frac{AP}{DP}$的值；
【应用】在【探究】的条件下，若$CD = 2$，$AC = 6$，求$BP$的长．

答案： 解：【猜想】$ \frac { 3 } { 2 } $ 【探究】过点 $ A $ 作 $ A F // B C $，交 $ B E $ 的延长线于点 $ F $。$ \because B E $ 是边 $ A C $ 上的中线，$ \therefore \frac { A E } { C E } = 1 $。$ \because C D : B C = 1 : 2 $，$ \therefore $ 设 $ C D = k $，则 $ B C = 2 k $，$ \therefore B D = C D + B C = 3 k $。$ \because A F // B C $，$ \therefore \triangle A E F \backsim \triangle C E B $，$ \therefore \frac { A F } { C B } = \frac { A E } { C E } = 1 $，即 $ A F = B C = 2 k $。$ \because A F // B D $，$ \therefore \triangle A P F \backsim \triangle D P B $，$ \therefore \frac { A P } { D P } = \frac { A F } { D B } = \frac { 2 k } { 3 k } = \frac { 2 } { 3 } $。【应用】$ \because B E $ 是边 $ A C $ 上的中线，$ C D = 2 $，$ A C = 6 $，$ C D : B C = 1 : 2 $，$ \therefore C E = \frac { 1 } { 2 } A C = 3 $，$ B C = 2 C D = 4 $。在 $ \mathrm { Rt } \triangle B C E $ 中，$ B E = \sqrt { C E ^ { 2 } + B C ^ { 2 } } = 5 $。易得 $ B F = 2 B E = 10 $。由【探究】知 $ \triangle A P F \backsim \triangle D P B $，$ \therefore \frac { P F } { P B } = \frac { A P } { D P } = \frac { 2 } { 3 } $，$ \therefore B P = \frac { 3 } { 5 } B F = \frac { 3 } { 5 } \times 10 = 6 $。