《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

8. (2025·无锡期中)如图,在△ABC中,AB= AC,∠BAC= 90°,直角∠EPF的顶点P是BC中点,PE,PF分别交边AB,AC于点E,F.给出以下四个结论:①AE= CF;②△EPF是等腰直角三角形;③S四边形AEPF= $\frac{1}{2}$S△ABC;④EF＞AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的有 ()

A. 1个
B. 2个
C. 3个
D. 4个

答案： C 解析：
∵AB=AC，∠BAC=90°，P是BC中点，
∴AP⊥BC，∠B=45°，
∴BP=AP，∠B=∠BAP=∠PAF=45°。
∵∠APB=∠EPF=90°，
∴∠BPE=90°−∠EPA=∠APF。在△BPE与△APF中，$\begin{cases}∠B=∠PAF，\\BP=AP，\\∠BPE=∠APF，\end{cases}$
∴△BPE≌△APF，
∴BE=AF，EP=FP，S△BPE=S△APF，
∴AB−BE=AC−AF，即AE=CF，△EPF是等腰直角三角形，故①②正确；
∵S四边形AEPF=S△AEP+S△APF=S△AEP+S△BPE=S△ABP=$\frac{1}{2}$S△ABC，故③正确；由勾股定理得AB²=BP²+AP²=2AP²，
∴AP²=$\frac{1}{2}$AB²=$\frac{1}{2}$(AE+BE)²。
∵EF²=AE²+AF²=AE²+BE²，
∴EF²−AP²=AE²+BE²−$\frac{1}{2}$(AE+BE)²=$\frac{1}{2}$(AE−BE)²≥0，
∴EF≥AP，故④错误。故选C。

9. (2025·苏州期中)如图,△ABC中,∠ACB= 90°,BC= 3,AC= 4,点D是AB的中点,将△ACD沿CD翻折得到△ECD,连接AE,BE,则线段BE的长等于______.

答案：
$\frac{7}{5}$ 解析：如图，延长CD交AE于点H，在Rt△ABC中，由勾股定理得AB=$\sqrt{AC²+BC²}$=$\sqrt{4²+3²}$=5。
∵D为AB的中点，
∴AD=BD=DC=$\frac{1}{2}$AB=$\frac{5}{2}$，由翻折的性质可知，AC=CE，AD=DE，∠ACH=∠ECH，
∴CH是AE的垂直平分线，
∴∠AHC=90°，AE=2AH，设DH=x，则CH=$\frac{5}{2}$+x，在Rt△ACH中，由勾股定理得AH²=AC²−CH²=4²−$(\frac{5}{2}+x)^2$，在Rt△ADH中，由勾股定理得AH²=AD²−DH²=$(\frac{5}{2})^2−x²$，
∴4²−$(\frac{5}{2}+x)^2$=$(\frac{5}{2})^2−x²$，解得x=$\frac{7}{10}$，
∴AH=$\sqrt{(\frac{5}{2})^2−(\frac{7}{10})^2}$=$\frac{12}{5}$，
∴AE=2AH=$\frac{24}{5}$。
∵AD=DE=BD，
∴∠DAE=∠DEA，∠DEB=∠DBE。
∵∠DAE+∠DEA+∠DEB+∠DBE=180°，
∴∠AEB=∠DEA+∠DEB=90°，
∴BE=$\sqrt{AB²−AE²}$=$\sqrt{5²−(\frac{24}{5})^2}$=$\frac{7}{5}$。

10. (2024·盐城期中)如图,在Rt△ABC中,∠ACB= 90°,AC= BC= 6,点D在边BC上,BD= 2,动点P在AB边上,连接PD,PC,当PC+PD的结果为整数时,此时点P的个数为______.

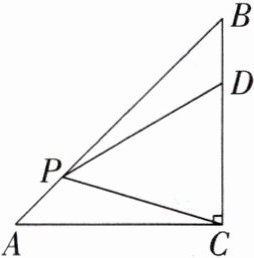
答案：
9 解析：如图，作△ABC′≌△ABC，点D′在线段BC′上，且BD′=BD=2，连接AD′，连接CD′交AB于点P1，
∵在Rt△ABC中，∠ACB=90°，AC=BC=6，△ABC′≌△ABC，
∴∠AC′B=∠ACB=90°，∠D′BP=∠DBP=$\frac{180°−90°}{2}$=45°，在△D′BP和△DBP中，$\begin{cases}BD′=BD，\\∠D′BP=∠DBP，\\BP=BP，\end{cases}$
∴△D′BP≌△DBP(SAS)，
∴PD′=PD，
∴PC+PD=PC+PD′，当点C，P，D′在同一直线上时，即点P运动到点P1时PC+PD最小，且最小值为$\sqrt{BC²+BD′²}$=$\sqrt{6²+2²}$=$\sqrt{40}$。当点P运动到和点B重合时，PC+PD=6+2=8。当点P运动到和点A重合时，PC+PD=6+$\sqrt{6²+(6−2)^2}$=$\sqrt{52}$+6。
∵36＜40＜49，49＜52＜64，
∴6＜$\sqrt{40}$＜7，7＜$\sqrt{52}$＜8，
∴13＜$\sqrt{52}$+6＜14。
∴线段P1B上有2个点P的位置，使得PC+PD的结果为整数；线段P1A上有7个点P的位置，使得PC+PD的结果为整数，
∴当PC+PD的结果为整数时，此时点P的个数为9。

11. 【概念认识】
定义:如果一个点能与另外两个点构成直角三角形,那么称这个点为另外两个点的勾股点.当这个点是直角的顶点时,这个点又称为强勾股点.
如图①,在Rt△ABC中,∠C= 90°,A是B,C两点的勾股点,B是A,C两点的勾股点,C是A,B两点的勾股点,也是强勾股点.

【概念运用】
(1)如图②,方格纸中的每个小正方形的边长均为1,A,B两点均在格点上,线段CD上的8个格点中,是A,B两点的勾股点的有______个.
(2)如图③,在△ABC中,CD⊥AB,垂足为D,若AD= 1,BD= 4,CD= 2,求证:C是A,B两点的强勾股点.
【拓展提升】
(3)如图④,在Rt△ABC中,∠C= 90°,AC= 6,BC= 4,D是AC的中点,P是射线BD上一个动点,当点P是Rt△ABC任意两个顶点的强勾股点时,直接写出BP的长.

答案：

(1)4 解析：如图①，G，H，T，R四点与A，B两点能构成四个直角三角形，
∴图中是A，B两点的勾股点的有4个。

(2)
∵CD⊥AB，
∴∠CDA=∠CDB=90°。在Rt△ACD中，由勾股定理得AD²+DC²=AC²，
∴AC²=1²+2²=5。在Rt△BCD中，由勾股定理得CD²+BD²=BC²，
∴BC²=2²+4²=20。在△ACB中，AC²+BC²=5+20=25。又
∵AB²=5²=25，
∴AC²+BC²=AB²。
∴由勾股定理逆定理得△ACB是直角三角形，且∠ACB=90°，
∴C是A，B两点的强勾股点。
(3)BP的长为2或$\frac{16}{5}$或$\frac{34}{5}$或8. 解析：当点P是A，C两个顶点的强勾股点，且点P在△ABC内时，如图②，
∵D为AC的中点，∠APC=90°，
∴PD=CD=$\frac{1}{2}$AC=3。
∵BC=4，
∴BD²=BC²+CD²=5²，
∴BD=5，
∴BP=BD−PD=5−3=2。当点P是B，C两个顶点的强勾股点时，如图③，
∵S△BCD=$\frac{1}{2}$BC·CD=$\frac{1}{2}$BD·CP，
∴CP=$\frac{BC·CD}{BD}$=$\frac{4×3}{5}$=$\frac{12}{5}$。
∴BP²=BC²−CP²=4²−$(\frac{12}{5})^2$=$(\frac{16}{5})^2$，
∴BP=$\frac{16}{5}$。当点P是A，B两个顶点的强勾股点时，如图④，
∵BC=4，AC=6，
∴AB²=BC²+AC²=4²+6²=52。设DP=x，则AD²−PD²=AB²−BP²，
∴3²−x²=52−(5+x)²，
∴x=$\frac{9}{5}$，
∴DP=$\frac{9}{5}$，
∴BP=BD+DP=5+$\frac{9}{5}$=$\frac{34}{5}$。当点P是A，C两个顶点的强勾股点，且点P在△ABC外时，如图⑤，
∵D为AC的中点，
∴AD=CD=DP=3，
∴BP=BD+DP=5+3=8。综上所述，BP的长为2或$\frac{16}{5}$或$\frac{34}{5}$或8。