《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

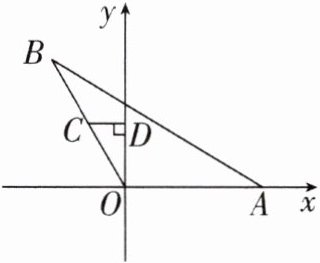
7. 如图,在$\triangle OAB$中,已知$OA= OB= 4$,$∠AOB= 120^{\circ}$.点C为OB的中点,过点C作$CD⊥y$轴,垂足为D.将$\triangle OCD$向右平移,当点C的对应点$C'$落在AB边上时,点D的对应点$D'$的坐标为 ()

A. $(2,\sqrt{2})$
B. $(2,\sqrt{3})$
C. $(3,\sqrt{2})$
D. $(3,\sqrt{3})$

答案：
B　解析：如图，
∵OA=OB=4，∠AOB=120°，点C为OB的中点，
∴∠B=∠A=30°，OC=2，
∵∠AOD=90°，
∴∠COD=30°，
∴CD=$\frac{1}{2}$OC=1，
∴OD=√3，
∴点D的坐标为(0,√3)。将△OCD向右平移，当点C的对应点C'落在AB边上时，O'C'=OC=2，可得∠C'O'A=∠AOB=120°，
∵∠A=30°，
∴∠O'C'A=∠A=30°，
∴O'C'=O'A=2，
∴OO'=4−2=2，
∴点D的对应点D'的坐标为(2,√3)。故选B。

8. (2024·大连模拟)如图,已知点A的坐标为$(-1,3)$,点B在x轴上,把$\triangle OAB$沿x轴向右平移到$\triangle DEF$,若平行四边形AEFB的面积为6,则点E的坐标为____.

答案： (1,3)　解析：
∵点A的坐标为(−1,3)，四边形AEFB的面积为6，
∴平行四边形AEFB的高为3，底为6÷3=2，即△OAB沿x轴向右平移到△DEF，平移的距离为2，将点A(−1,3)向右平移2个单位长度，所得到的点E的坐标为(1,3)。

9. 如图,在平面直角坐标系中,对正方形ABCD及其内部的每个点进行如下操作:先把每个点的横、纵坐标都乘$\frac{1}{2}$,再将得到的点先向右平移m个单位长度,再向上平移n个单位长度$(m＞0,n＞0)$,得到正方形$A'B'C'D'$及其内部的点,其中点A,B的对应点分别为$A',B'$.已知正方形ABCD内部的一点F经过上述操作后得到的对应点$F'$与点F重合,则点F的坐标是____.

答案： (1,4)　解析：由题可知，由点A到A'，可得方程组$\begin{cases}-3×\frac{1}{2} + m = -1\\0×\frac{1}{2} + n = 2\end{cases}$，由B到B'可得方程组$\begin{cases}3×\frac{1}{2} + m = 2\\0×\frac{1}{2} + n = 2\end{cases}$，解得$\begin{cases}m = \frac{1}{2}\\n = 2\end{cases}$，设点F的坐标为(x,y)，则F'的坐标为($\frac{1}{2}$x + $\frac{1}{2}$,$\frac{1}{2}$y + 2)，由点F'，F重合，得方程组$\begin{cases}\frac{1}{2}x + \frac{1}{2} = x\\\frac{1}{2}y + 2 = y\end{cases}$，解得$\begin{cases}x = 1\\y = 4\end{cases}$，即F(1,4)。

10. (2024·重庆期末)阅读材料:对于平面直角坐标系xOy中的图形G和图形G上的任意一点$P(x,y)$,给出如下定义:将点$P(x,y)平移到P'(x+a,y-a)$称为将点P进行“a型平移”,点$P'$称为将点P进行“a型平移”的对应点;将图形G上的所有点进行“a型平移”称为将图形G进行“a型平移”.
例如:将点$P(x,y)平移到P'(x+1,y-1)$称为将点P进行“1型平移”,将点$P(x,y)平移到P'(x-1,y+1)$称为将点P进行“-1型平移”.
已知点$A(1,1)和点B(3,1)$.
(1)将点$A(1,1)$进行“1型平移”后的对应点$A'$的坐标为____;将线段AB进行“-1型平移”后得到线段$A'B'$,线段$A'B'$的中点坐标为____.
(2)若线段AB进行“a型平移”后与坐标轴有公共点,求a的取值范围.
(3)已知点$C(4,0)$,$D(6,-2)$,将线段CD进行“1型平移”后得到的对应线段为$C'D'$,在坐标轴上确定一点M,使得$S_{\triangle MC'D'}= 5S_{\triangle ABO}$,请写出所有符合条件的点M的坐标,并选择一种情况写出求解过程.

答案：

(1)(2,0)　(1,2)
(2)线段AB进行“a型平移”后，则A'(1+a,1−a)，B'(3+a,1−a)，当线段A'B'与x轴有公共点，即1−a=0，解得a=1；当线段A'B'与y轴有公共点，即1+a≤0，3+a≥0，解得−3≤a≤−1，故a的取值范围为−3≤a≤−1或a=1。
(3)
∵点C(4,0)，D(6,−2)，将线段CD进行“1型平移”后得到的对应线段为C'D'，
∴C'(5,−1)，D'(7,−3)。
∵A(1,1)，B(3,1)，O(0,0)，
∴AB=3−1=2，
∴$S_{\triangle ABO} = \frac{1}{2}×AB×y_A = \frac{1}{2}×2×1 = 1$，
∴$S_{\triangle MC'D'} = 5S_{\triangle ABO} = 5$。
①当点M在y轴上时，设M(0,a)，则$S_{\triangle MC'D'} = \frac{1}{2}×5×(a + 3) = 5$，解得a=−1，
∴M1(0,−1)；
②当点M在x轴上时，设M(b,0)，则$S_{\triangle MC'D'} = S_{\triangle MCD'} - S_{\triangle MCC'} = 5$，
∴$\frac{1}{2}MC·y_{D'} - \frac{1}{2}MC·y_{C'} = \frac{1}{2}MC(y_{D'} - y_{C'}) = \frac{1}{2}×|b - 4|×(3 - 1) = |b - 4| = 5$，解得b=−1或b=9，
∴M2(9,0)，M3(−1,0)；
③当点M在y轴上且在x轴上方时，设M(0,m)，则$\frac{7(m + 3)}{2} = 5 + \frac{5(m + 1)}{2} + \frac{(5 + 7)×2}{2}$，解得m=9，
∴M4(0,9)。综上，点M的坐标为M1(0,−1)，M2(9,0)，M3(−1,0)，M4(0,9)。