《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

8. 如图,$AE⊥AB$,且$AE= AB,BC⊥CD$,且$BC= CD,EF⊥AC,BG⊥AC,DH⊥AC$,垂足分别是F,G,H,请按照图中所标注的数据:$EF= 6,BG= 3,DH= 4$,计算图中实线所围成的图形的面积S是____.

答案： 50 解析: $∵ ∠EAF + ∠BAG = 90°$，$∠EAF + ∠AEF = 90°$，$∴ ∠BAG = ∠AEF$。在 $△AEF$ 和 $△BAG$ 中，$\begin{cases}∠EFA = ∠AGB = 90° \\ ∠AEF = ∠BAG \\ AE = BA \end{cases}$，$∴ △AEF ≌ △BAG(AAS)$。同理 $△BCG ≌ △CDH$，$∴ AF = BG$，$AG = EF$，$GC = DH$，$BG = CH$。$∵$ 梯形 $DEFH$ 的面积 $ = \frac{1}{2}(EF + DH) \cdot FH = 80$，$S_{△AEF} = S_{△ABG} = \frac{1}{2}AF \cdot EF = 9$，$S_{△BCG} = S_{△CDH} = \frac{1}{2}CH \cdot DH = 6$，$∴$ 题图中实线所围成的图形的面积 $S = 80 - 2×9 - 2×6 = 50$。

9. (2024·无锡校级月考)如图,$AO⊥OM,OA= 4$,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰直角三角形OBF、等腰直角三角形ABE,连接EF交OM于点P,当点B在射线OM上移动时,BP的长度为____.

答案： 2 解析:过点 $E$ 作 $EN ⊥ BM$，垂足为 $N$，$∵ ∠AOB = ∠ABE = ∠BNE = 90°$，$∴ ∠ABO + ∠BAO = ∠ABO + ∠NBE = 90°$，$∴ ∠BAO = ∠NBE$。$∵ △ABE$、$△BFO$ 均为等腰直角三角形，$∴ AB = BE$，$BF = BO$。在 $△ABO$ 和 $△BEN$ 中，$\begin{cases}∠BAO = ∠EBN \\ ∠AOB = ∠BNE \\ AB = BE \end{cases}$，$∴ △ABO ≌ △BEN(AAS)$，$∴ BO = NE$，$BN = AO$。$∵ BO = BF$，$∴ BF = NE$。在 $△BPF$ 和 $△NPE$ 中，$\begin{cases}∠FBP = ∠ENP \\ ∠FPB = ∠EPN \\ BF = NE \end{cases}$，$∴ △BPF ≌ △NPE(AAS)$，$∴ BP = NP = \frac{1}{2}BN$。又 $∵ BN = AO$，$∴ BP = \frac{1}{2}AO = \frac{1}{2}×4 = 2$。

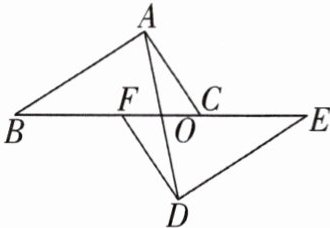
10. 如图,点B,F,C,E在一条直线上,$FB= CE,AB// ED,AC// FD$,AD交BE于O.
(1) 求证:AD与BE互相平分;
(2) 若$BF= 5,FC= 4$,直接写出OE的长.

答案：
(1) $∵ FB = CE$，$∴ FB + CF = CE + CF$，即 $BC = EF$。又 $∵ AB // ED$，$AC // FD$，$∴ ∠ABC = ∠DEF$，$∠ACB = ∠DFE$。在 $△ABC$ 和 $△DEF$ 中，$\begin{cases}∠ABC = ∠DEF \\ BC = EF \\ ∠ACB = ∠DFE \end{cases}$，$∴ △ABC ≌ △DEF(ASA)$，$∴ AC = DF$。在 $△AOC$ 和 $△DOF$ 中，$\begin{cases}∠AOC = ∠DOF \\ ∠ACO = ∠DFO \\ AC = DF \end{cases}$，$∴ △AOC ≌ △DOF(AAS)$，$∴ AO = DO$，$CO = FO$。$∵ BF = CE$，$∴ BO = EO$，$∴ AD$ 与 $BE$ 互相平分。
(2) $OE = 7$。解析: $∵ BF = CE = 5$，$FC = 4$，$∴ BE = BF + FC + CE = 14$，$∴ BO = OE = \frac{1}{2}BE = 7$。

11. 阅读与证明:在一个三角形中,如果有两个角相等,那么这两个角所对的边也相等.如图①,在$△ABC$中,如果$∠B= ∠C$,那么$AB= AC$,这一结论可以说明如下:
解:过点A作$AD⊥BC$于D,则$∠ADB= ∠ADC= 90^{\circ }$,在$△ABD和△ACD$中,$∠B= ∠C,∠ADB= ∠ADC,AD= AD,\therefore △ABD\cong △ACD,\therefore AB= AC$.
请你仿照上述方法在图②中再选一种方法说明以上结论.
操作:如图③,点O为线段MN的中点,直线PQ与MN相交于点O,过点M,N作一组平行线分别与PQ交于点$M',N'$,则线段$MM'一定等于NN'$.想一想,为什么?
根据上述阅读与证明的结论以及操作得到的经验完成下列探究活动.
探究:如图④,在四边形ABCD中,$AB// DC$,E为BC边的中点,$∠BAE= ∠EAF$,AF与DC的延长线相交于点F.试探究线段AB与AF,CF之间的数量关系,并证明你的结论.

电

答案：
阅读与证明:如图①，作 $∠BAC$ 的平分线 $AD$，交 $BC$ 于 $D$，则 $∠BAD = ∠CAD$。在 $△ABD$ 和 $△ACD$ 中，$\begin{cases}∠BAD = ∠CAD \\ ∠B = ∠C \\ AD = AD \end{cases}$，$∴ △ABD ≌ △ACD(AAS)$，$∴ AB = AC$。(合理即可)

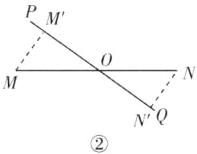
操作:如图②，$∵ MM' // NN'$，$∴ ∠MM'O = ∠NN'O$。$∵$ 点 $O$ 为线段 $MN$ 的中点，$∴ OM = ON$。在 $△MOM'$ 和 $△NON'$ 中，$\begin{cases}∠MM'O = ∠NN'O \\ ∠MOM' = ∠NON' \\ OM = ON \end{cases}$，$∴ △MOM' ≌ △NON'(AAS)$，$∴ MM' = NN'$。
探究: $AB = AF + CF$。证明:如图③，连接 $FE$ 并延长，交 $AB$ 于点 $G$，$∵ AB // DC$，$∴ ∠B = ∠ECF$。$∵ E$ 为 $BC$ 边的中点，$∴ BE = CE$。在 $△BEG$ 和 $△CEF$ 中，$\begin{cases}∠B = ∠ECF \\ BE = CE \\ ∠BEG = ∠CEF \end{cases}$，$∴ △BEG ≌ △CEF(ASA)$，$∴ EG = EF$，$BG = CF$。延长 $AE$ 到 $H$，使 $AE = EH$，连接 $FH$，在 $△AEG$ 和 $△HEF$ 中，$\begin{cases}AE = HE \\ ∠AEG = ∠HEF \\ EG = EF \end{cases}$， $∴ △AEG ≌ △HEF(SAS)$，$∴ AG = HF$，$∠BAE = ∠H$。$∵ ∠BAE = ∠EAF$，$∴ ∠H = ∠EAF$。由“阅读与证明”中证明的结论可得 $AF = HF$，$∴ AG = AF$。$∵ AB = AG + BG$，$∴ AB = AF + CF$。