《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

3. 在$△ABC$中,$AB= AC,∠ABC= α$,点 D 是直线 BC 上一点,点 C 关于射线 AD 的对称点为点 E.作直线 BE 交射线 AD 于点 F.连接 CF.
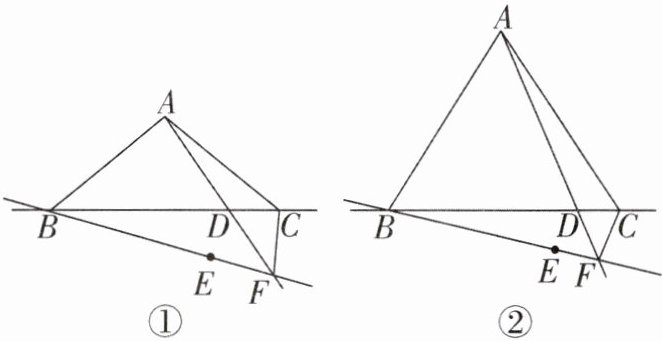
(1)如图①,点 D 在线段 BC 上,求$∠AFB$的大小(用含α的代数式表示).
(2)如果$∠α=60^{\circ }.$
①如图②,当点 D 在线段 BC 上时,用等式表示线段 AF,BF,CF 之间的数量关系,并证明;
②如图③,当点 D 在线段 CB 的延长线上时,补全图形,写出线段 AF,BF,CF 之间的数量关系.

答案：

(1) 如图①, 连接 $ AE $, $ CE $, $ \because $ 点 $ E $ 为点 $ C $ 关于 $ AD $ 的对称点, $ \therefore AE = AC $, $ EF = FC $, $ \angle EAD = \angle CAD $. 设 $ \angle EAD = \angle CAD = x $, 则 $ \angle CAE = 2x $. $ \because AB = AC $, $ \therefore \angle ACB = \angle ABC = \alpha $, $ \therefore \angle BAE = 180^\circ - 2x - 2\alpha $, $ \therefore \angle ABE + \angle AEB = 2x + 2\alpha $. $ \because AE = AB $, $ \therefore \angle ABE = \angle AEB = x + \alpha $, $ \therefore \angle AFB = \angle AEB - \angle EAD = \alpha $.
　　
(2) ① $ AF = BF + CF $. 证明如下: 如图②, 延长 $ FB $ 至点 $ G $, 使 $ FG = FA $, 连接 $ AG $. $ \because AB = AC $, $ \therefore \angle ABC = \alpha = 60^\circ $, $ \therefore \triangle ABC $ 为等边三角形, $ \angle BAC = 60^\circ $. 由
(1)知, $ \angle AFB = \alpha = 60^\circ $, $ \therefore \triangle AFG $ 为等边三角形, $ \therefore AG = AF $, $ \angle GAF = 60^\circ $, $ \therefore \angle GAB = \angle FAC $. 在 $ \triangle ABG $ 和 $ \triangle ACF $ 中, $ \left\{ \begin{array} { l } { AG = AF, } \\ { \angle GAB = \angle FAC, } \\ { AB = AC, } \end{array} \right. $ $ \therefore \triangle ABG \cong \triangle ACF (SAS) $, $ \therefore BG = CF $, $ \therefore CF + BF = BG + BF = GF $. $ \because GF = AF $, $ \therefore AF = BF + CF $.
②补全图形如图③所示. $ CF = AF + BF $. 连接 $ AE $, $ EC $, $ \because $ 点 $ E $ 为点 $ C $ 关于 $ AD $ 的对称点, $ \therefore AE = AC $, $ EF = FC $, $ \angle EAD = \angle CAD $. 设 $ \angle EAD = \angle CAD = x $, 则 $ \angle CAE = 2x $. $ \because AB = AC = AE $, $ \therefore \angle ACB = \angle ABC = \angle BAC = 60^\circ $, $ \therefore \angle DAB = x - 60^\circ $, $ \therefore \angle EAB = x + x - 60^\circ = 2x - 60^\circ $. $ \because AE = AB $, $ \therefore \angle ABE = \angle AEB = \frac { 180 ^ { \circ } - 2 x + 60 ^ { \circ } } { 2 } = 120 ^ { \circ } - x $, $ \therefore \angle AFE = \angle DAB + \angle ABE = x - 60 ^ { \circ } + 120 ^ { \circ } - x = 60 ^ { \circ } $. 在 $ BE $ 上取点 $ G $, 使得 $ FG = FA $, 连接 $ AG $, $ \therefore \triangle AFG $ 为等边三角形, $ \therefore AG = AF $, $ \angle GAF = 60 ^ { \circ } $, $ \therefore \angle GAE = \angle FAB = x - 60 ^ { \circ } $. 在 $ \triangle AGE $ 和 $ \triangle AFB $ 中, $ \left\{ \begin{array} { l } { AG = AF, } \\ { \angle GAE = \angle FAB, } \\ { AE = AB, } \end{array} \right. $ $ \therefore \triangle AGE \cong \triangle AFB (SAS) $, $ \therefore BF = EG $, $ \therefore EF = EG + FG = BF + AF $, $ \therefore CF = EF = AF + BF $.
　　　　　　　　　　　　　　　　

4. (2024·南京期中)通过对下面数学模型的研究学习,解决下列问题:
【模型理解】
(1)如图①,$△ABC,△ADE$共顶点 A,$AB= AC,AD= AE,∠BAC= ∠DAE$,连接 BD,CE.由$∠BAC-∠DAC= ∠DAE-∠DAC$,得$∠BAD= ∠CAE$.又$AB= AC,AD= AE$,可以推理得到$△ABD\cong △ACE$,进而得到$BD= $____,$∠ABD= $____.
【问题研究】(2)小明同学在思考完上述问题后,解决了下面的尺规作图问题.
如图②,已知直线 a,b 及点 P,a 与 b 不平行.作等腰直角三角形 PAB,使得点 A,B 分别在直线 a,b 上.小明同学作法简述如下:如图③,过点 P 作$PD⊥a$,垂足为点 D,以 P 为直角顶点作等腰直角三角形 PDE,过点 E 作$EB⊥PE$,交 b 于点 B,在 a 上截取$DA= BE$,连接 AB.$△PAB$即为所要求作的等腰直角三角形.
请证明小明的作法是正确的.
【深入研究】小明同学经过研究发现:在上题条件下,也能作出等边三角形 PAB,使得点 A,B 分别在直线 a,b 上.
(3)请你简述作法,并在图④中画出示意图.(不需要尺规作图)

答案：

(1) $ CE $ $ \angle ACE $ 解析: $ \because \angle BAC = \angle DAE $, $ \therefore \angle BAC - \angle DAC = \angle DAE - \angle DAC $, $ \therefore \angle BAD = \angle CAE $, 在 $ \triangle ABD $ 和 $ \triangle ACE $ 中, $ \left\{ \begin{array} { l } { AB = AC, } \\ { \angle BAD = \angle CAE, } \\ { AD = AE, } \end{array} \right. $ $ \therefore \triangle ABD \cong \triangle ACE (SAS) $, $ \therefore BD = CE $, $ \angle ABD = \angle ACE $. 故答案为 $ CE $, $ \angle ACE $.
(2) $ \because \triangle PDE $ 是以 $ P $ 为直角顶点的等腰直角三角形, $ \therefore PE = PD $, $ \angle DPE = 90 ^ { \circ } $. $ \because EB \perp PE $, $ PD \perp a $, $ \therefore \angle PEB = \angle PDA = 90 ^ { \circ } $, 在 $ \triangle PEB $ 和 $ \triangle PDA $ 中, $ \left\{ \begin{array} { l } { EB = DA, } \\ { \angle PEB = \angle PDA, } \\ { PE = PD, } \end{array} \right. $ $ \therefore \triangle PEB \cong \triangle PDA (SAS) $, $ \therefore PB = PA $, $ \angle BPE = \angle APD $, $ \therefore \angle APB = \angle APE + \angle BPE = \angle APE + \angle APD = \angle DPE = 90 ^ { \circ } $, $ \therefore \triangle PAB $ 即为所要求作的等腰直角三角形.
(3) 如图, $ \triangle PAB $ 即为所求.
　　　　　　　
作法: 1. 作 $ PF \perp a $ 于点 $ F $;
2. 以 $ PF $ 为边在 $ PF $ 右侧作等边三角形 $ PFG $;
3. 以 $ FG $ 为边在 $ FG $ 上方作等边三角形 $ FGH $;
4. 连接 $ PH $ 交直线 $ a $ 于点 $ I $;
5. 连接并延长 $ IG $ 交直线 $ b $ 于点 $ B $;
6. 在射线 $ FI $ 上取一点 $ A $, 连接 $ PB $, $ PA $, 使 $ PA = PB $, 连接 $ AB $.