《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

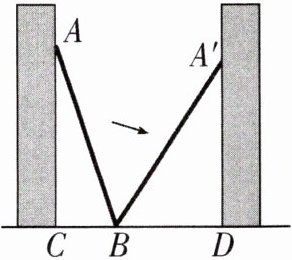
7. (绍兴中考)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 0.7 米,顶端距离地面 2.4 米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面 2 米,则小巷的宽度为()

A. 0.7 米
B. 1.5 米
C. 2.2 米
D. 2.4 米

答案： C　解析:在Rt△ACB中,
∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB²=0.7²+2.4²=6.25=A'B².在Rt△A'BD中,
∵∠A'DB=90°,A'D=2米,BD²+A'D²=A'B²,
∴BD²+2²=6.25,
∴BD²=2.25.
∵BD＞0,
∴BD=1.5米,
∴CD=BC+BD=0.7+1.5=2.2(米).故选C.

8. 如图是一种饮料的包装盒,长、宽、高分别为 4 cm、3 cm、12 cm,现有一长为 16 cm 的吸管插入到盒的底部,则吸管露在盒外的部分 h 的取值范围是()

A. 3 cm ＜ h ＜ 4 cm
B. 3 cm ≤ h ≤ 4 cm
C. 2 cm ≤ h ≤ 4 cm
D. h = 4 cm

答案： B　解析:①当吸管放进盒里垂直于底面时，露在盒外的长度最长，最长为16−12=4(cm);②露出部分最短时吸管与底面对角线和高正好组成直角三角形,底面对角线为5cm,高为12cm,由勾股定理易得盒里面吸管长为13cm,则露在盒外的长度为16−13=3(cm),则可得吸管露在盒外的部分h的取值范围是3cm≤h≤4cm.故选B.

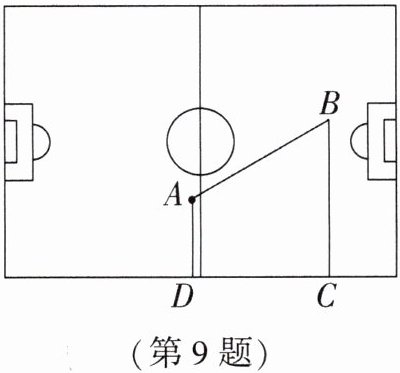
9. 新情境 (2025·昭通期末)足球是世界上最受欢迎的运动项目之一,如图,球员 A 向边线 CD 传球,传球落点在边线 CD 上任何位置都能被边线球员接住球,而边线球员不运球直接传给球员 B,图中四边形 ABCD 为直角梯形,AD= 5,AB= BC= 10,∠B= 60°,则两次传球中足球飞过的最短路径为()

A. 15
B. 10√3
C. 20
D. 20√3

答案：
B　解析:如图,作点A关于CD的对称点E,连接BE交CD于点O,连接AO,过点A作AF⊥BE于点F,
∴DE=AD=5,AO=EO,
∴AE=AD+DE=10=AB,AO+BO=EO+BO=BE,
∴∠E=∠ABE,两次传球中足球飞过的最短路径长等于BE，依题意得AD//BC,
∴∠E=∠CBE,
∴∠E=∠CBE=∠ABE.
∵∠ABC=∠ABE+∠CBE=60°,
∴∠ABE=30°.又AF⊥BE,
∴AF=$\frac{1}{2}$AB=5,
∴BF=$\sqrt{AB²−AF²}$=5√3.又AE=AB,
∴BE=2BF=10√3,即两次传球中足球飞过的最短路径为10√3.故选B.

10. (2025·盐城期中)《九章算术》是古代东方数学代表作,书中记载：今有开门去阃(读 kǔn,门槛的意思)一尺,不合二寸,问门广几何? 题目大意是：如图①、②(图②为图①的平面示意图),推开双门,双门间隙 CD 的距离为 2 寸,点 C 和点 D 距离门槛 AB 都为 1 尺(1 尺 = 10 寸),则 AB 的长是______寸.

答案：
101　解析:如图,设DE⊥AB于点E.由题意,得OA=OB=AD=BC.设OA=OB=AD=BC=r寸,则AB=2r寸,DE=10寸,OE=$\frac{1}{2}$CD=1寸,AE=(r−1)寸,在Rt△ADE中,AE²+DE²=AD²,即(r−1)²+10²=r²,解得r=50.5,
∴2r=101,
∴AB=101寸.

11. 如图,铁路 MN 和公路 PQ 在点 O 处交会,公路 PQ 上点 A 距离点 O 是 270 m,与 MN 这条铁路的距离是 200 m.如果火车行驶时,周围 250 m 以内会受到噪音的影响,那么火车在铁路 MN 上沿 ON 方向以 20 m/s 的速度行驶时,点 A 处受噪音影响的时间是______.

答案：
15s解析:如图,过点A作AC⊥ON,设火车行驶到点B处时,A点处开始受噪音影响，火车行驶到点D处时，A点处开始不受噪音影响,则AB=AD=250m.
∵公路PQ上点A距离点O是270m,与MN这条铁路的距离是200m,
∴AC=200m.
∵AB=AD=250m,
∴由勾股定理得BC²=AB²−AC²=150²,
∴BC=150m.又CD²=AD²−AC²=150²,
∴CD=150m,
∴BD=BC+CD=300(m),
∴A处受噪音影响的时间为300÷20=15(s).

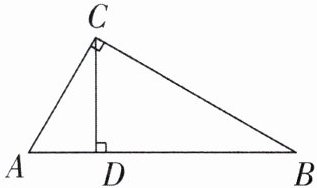
12. 教材变式 如图所示,直角三角形 ABC 的两条直角边长为 a,b,斜边上的高 CD 的长为 h,斜边长为 c.求证：$\frac{1}{a^{2}}+\frac{1}{b^{2}}= \frac{1}{h^{2}}$.

答案：
∵ab=ch,
∴h=$\frac{ab}{c}$，
∴$\frac{1}{a²}$+$\frac{1}{b²}$=$\frac{a²+b²}{a²b²}$=$\frac{c²}{a²b²}$=($\frac{c}{ab}$)²=($\frac{1}{h}$)²=$\frac{1}{h²}$.