《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

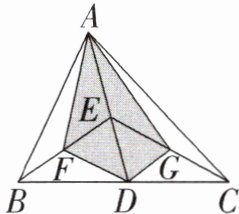
1. (2024·泰州期末)如图,$\triangle ABC$的面积是16,点D,E,F,G分别是BC,AD,BE,CE的中点,则四边形AFDG的面积是______.

答案： 8 解析: 因为 $ AD $ 为 $ \triangle ABC $ 中 $ BC $ 边的中线，$ S_{\triangle ABC} = 16 $，所以 $ S_{\triangle ABD} = S_{\triangle ACD} = \frac{1}{2} S_{\triangle ABC} = \frac{1}{2} \times 16 = 8 $。因为 $ BE $，$ CE $ 是 $ AD $ 的中线，所以 $ S_{\triangle ABE} = S_{\triangle BED} = \frac{1}{2} S_{\triangle ABD} = 4 $，$ S_{\triangle AEC} = S_{\triangle CED} = \frac{1}{2} S_{\triangle ACD} = 4 $，同理，$ S_{\triangle AEF} = \frac{1}{2} S_{\triangle ABE} = 2 $，$ S_{\triangle AEG} = \frac{1}{2} S_{\triangle AEC} = 2 $，$ S_{\triangle DEF} = \frac{1}{2} S_{\triangle BDE} = 2 $，$ S_{\triangle DEG} = \frac{1}{2} S_{\triangle CED} = 2 $，所以 $ S_{\text{四边形}AFDG} = S_{\triangle AEF} + S_{\triangle AEG} + S_{\triangle DEF} + S_{\triangle DEG} = 8 $。

2. 操作与实践.
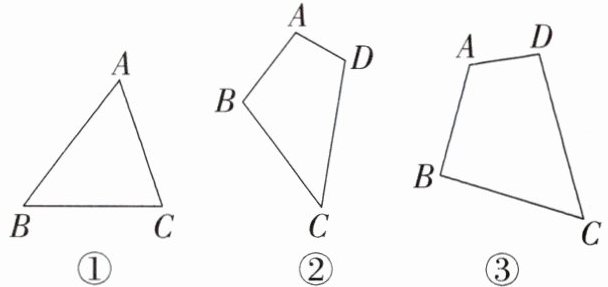
(1)如图①,请你在$\triangle ABC$中画一条线段,把$\triangle ABC$分成面积相等的两部分；
(2)如图②,请你按照(1)的方法把四边形ABCD分成面积相等的两部分；
(3)利用以上性质尝试在如图③所示的四边形ABCD中作一条线段,把四边形ABCD分成面积相等的两部分.(无需写出画图步骤和理由)

答案：
答案合理即可，如:
(1) 如图①，取 $ BC $ 的中点 $ D $，$ AD $ 为 $ BC $ 边上的中线，则 $ BD = CD $，根据等底同高的三角形面积相等，得 $ S_{\triangle ABD} = S_{\triangle ACD} $。
　　　　 　　 　　
(2) 如图②，连接 $ AC $，再取 $ AC $ 的中点 $ E $，连接 $ BE $，$ DE $，所以 $ S_{\triangle ADE} = S_{\triangle CDE} $，$ S_{\triangle ABE} = S_{\triangle BCE} $，所以 $ S_{\triangle ADE} + S_{\triangle ABE} = S_{\triangle CDE} + S_{\triangle BCE} $，所以 $ S_{\text{四边形}ABED} = S_{\text{四边形}BCDE} $。
(3) 如图③，连接 $ AC $，$ BD $，取 $ AC $ 的中点 $ O $，过点 $ O $ 作 $ OE // BD $ 交 $ CD $ 于 $ E $，连接 $ BE $，线段 $ BE $ 把四边形 $ ABCD $ 分成面积相等的两部分。
解析: 连接 $ OD $ 交 $ BE $ 于 $ F $，连接 $ OB $，由
(1) 知，$ S_{\triangle DBE} = S_{\triangle BDO} $（同底等高的三角形面积相等）。因为 $ S_{\triangle DBE} = S_{\triangle BDF} + S_{\triangle DEF} $，$ S_{\triangle BDO} = S_{\triangle BDF} + S_{\triangle OBF} $，所以 $ S_{\triangle DEF} = S_{\triangle OBF} $。因为点 $ O $ 是 $ AC $ 的中点，由
(2) 知，$ S_{\triangle ADO} = S_{\triangle CDO} $，$ S_{\triangle ABO} = S_{\triangle CBO} $，所以 $ S_{\triangle BCE} = S_{\triangle CBO} + S_{\triangle OBF} + S_{\triangle CEO} + S_{\triangle OEF} = S_{\triangle CBO} + S_{\triangle DEF} + S_{\triangle CEO} + S_{\triangle OEF} = S_{\triangle CBO} + S_{\triangle CDO} $，$ S_{\text{四边形}ABED} = S_{\text{四边形}ABFD} + S_{\triangle DEF} = S_{\triangle ABO} + S_{\triangle ADO} - S_{\triangle OBF} + S_{\triangle DEF} = S_{\triangle ABO} + S_{\triangle ADO} = S_{\triangle CBO} + S_{\triangle CDO} $。所以 $ S_{\triangle BCE} = S_{\text{四边形}ABED} $，即线段 $ BE $ 把四边形 $ ABCD $ 分成面积相等的两部分。

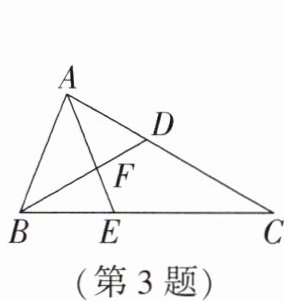
3. (2024·重庆期中)如图,在$\triangle ABC$中,D为AC上一点,E为BC上一点,$AD= \frac{2}{3}CD$,连接BD,AE交于点F.若$S_{\triangle ACE}= S_{\triangle BCD}$,$S_{\triangle ABC}= 15$,则$\triangle ABE$的面积为______.

答案： 6 解析: 因为 $ AD = \frac{2}{3} CD $，所以 $ AD = \frac{2}{5} AC $。因为 $ S_{\triangle ABC} = 15 $，所以 $ S_{\triangle ABD} = \frac{2}{5} S_{\triangle ABC} = \frac{2}{5} \times 15 = 6 $。因为 $ S_{\triangle ACE} = S_{\triangle BCD} $，所以 $ S_{\triangle ABE} = S_{\triangle ABD} = 6 $。

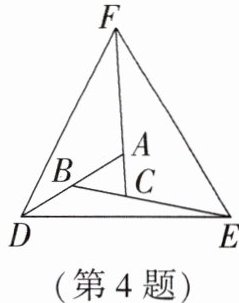
4. 如图,$\triangle ABC$中,分别延长边AB,BC,CA,使得$BD= AB$,$CE= 2BC$,$AF= 3CA$,若$\triangle ABC$的面积为2,则$\triangle DEF$的面积为______.

答案： 36 解析: 连接 $ AE $，$ CD $，因为 $ BD = AB $，所以 $ S_{\triangle ABC} = S_{\triangle BCD} = 2 $，则 $ S_{\triangle ACD} = 2 + 2 = 4 $。因为 $ AF = 3AC $，所以 $ FC = 4AC $，所以 $ S_{\triangle FCD} = 4S_{\triangle ACD} = 4 \times 4 = 16 $。同理可以求得 $ S_{\triangle ACE} = 2S_{\triangle ABC} = 4 $，则 $ S_{\triangle FCE} = 4S_{\triangle ACE} = 4 \times 4 = 16 $，$ S_{\triangle DCE} = 2S_{\triangle BCD} = 2 \times 2 = 4 $，所以 $ S_{\triangle DEF} = S_{\triangle FCD} + S_{\triangle FCE} + S_{\triangle DCE} = 16 + 16 + 4 = 36 $。

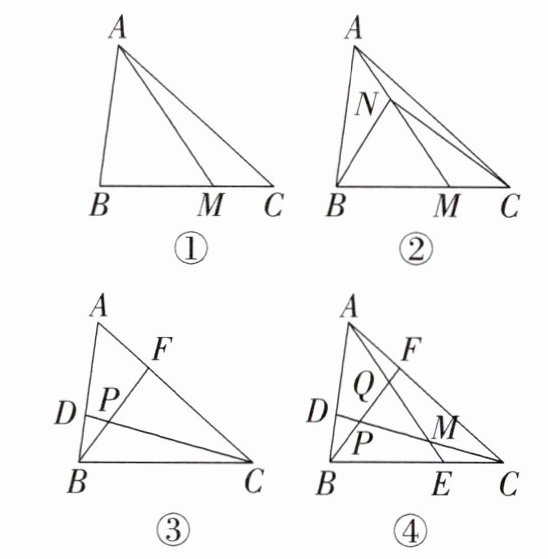
5. (1)【基础知识】我们知道：如果两个三角形的高相同,那么它们的面积比等于对应底边的比.如图①,点M是$\triangle ABC$的边BC上一点,试说明：$\frac{S_{\triangle ABM}}{S_{\triangle ACM}}= \frac{BM}{CM}$.
(2)【知识应用】如图②,$\triangle ABC$的边BC上有一点M,N为AM上任意一点,利用上述结论,猜想$\frac{S_{\triangle ABN}}{S_{\triangle ACN}}与\frac{BM}{CM}$之间的关系,请直接写出结论.
(3)【知识迁移】如图③,在$\triangle ABC$中,D,F分别在边AB,AC上,且$AD= 2DB$,$CF= 2AF$.若$\triangle ABC$的面积为1,求四边形ADPF的面积.
(4)【知识延伸】如图④,在$\triangle ABC$中,D,E,F分别在边AB,BC,CA上,且$AD= 2DB$,$BE= 2EC$,$CF= 2AF$,连接AE,BF,CD,交点为P,Q,M,若$\triangle PQM$的面积为1,则$\triangle ABC$的面积为______.

答案：

(1) 如图①，过点 $ A $ 作 $ AD \perp BC $ 于点 $ D $，则 $ S_{\triangle ABM} = \frac{1}{2} BM \cdot AD $，$ S_{\triangle ACM} = \frac{1}{2} CM \cdot AD $，所以 $ \frac{S_{\triangle ABM}}{S_{\triangle ACM}} = \frac{\frac{1}{2} BM \cdot AD}{\frac{1}{2} CM \cdot AD} = \frac{BM}{CM} $。
　　　　
(2) $ \frac{S_{\triangle ABN}}{S_{\triangle ACN}} = \frac{BM}{CM} $。解析: 由
(1) 得，$ \frac{S_{\triangle ABN}}{S_{\triangle BMN}} = \frac{AN}{MN} $，$ \frac{S_{\triangle ACN}}{S_{\triangle CMN}} = \frac{AN}{MN} $，所以 $ \frac{S_{\triangle ABN}}{S_{\triangle BMN}} = \frac{S_{\triangle ACN}}{S_{\triangle CMN}} $，所以 $ \frac{S_{\triangle ABN}}{S_{\triangle ACN}} = \frac{S_{\triangle BMN}}{S_{\triangle CMN}} = \frac{BM}{CM} $。
(3) 如图②，连接 $ PA $，设 $ S_{\triangle BPD} = a $，$ S_{\triangle APF} = b $，$ S_{\triangle BCP} = c $。因为 $ AD = 2DB $，$ CF = 2AF $，所以 $ S_{\triangle APD} = 2S_{\triangle BPD} = 2a $，$ S_{\triangle CPF} = 2S_{\triangle APF} = 2b $，$ S_{\triangle ACD} = 2S_{\triangle BCD} $，$ S_{\triangle BCF} = 2S_{\triangle ABF} $，所以 $ 2a + b + 2b = 2(a + c) $，$ 2b + c = 2(a + 2a + b) $，所以 $ 2c = 3b $，$ c = 6a $，所以 $ 2 \times 6a = 3b $，所以 $ b = 4a $。因为 $ \triangle ABC $ 的面积为 1，所以 $ 3a + 3b + c = 1 $，即 $ 3a + 12a + 6a = 1 $，解得 $ a = \frac{1}{21} $。所以 $ S_{\text{四边形}ADPF} = 2a + b = 6a = 6 \times \frac{1}{21} = \frac{2}{7} $。
(4) 7 解析: 如图③，连接 $ PA $，$ QC $，设 $ S_{\triangle BPD} = m $，$ S_{\triangle AFQ} = n $，由
(3) 得，$ S_{\text{四边形}ADPF} = 6m = S_{\triangle BCP} $，$ S_{\triangle CPF} = 8m $，同理，$ S_{\triangle ABQ} = 6S_{\triangle AFQ} = 6n $，则 $ m + 6m = n + 6n $，所以 $ m = n $，即 $ S_{\triangle BPD} = S_{\triangle AFQ} = m $。同理，$ S_{\triangle CME} = S_{\triangle BPD} = S_{\triangle AFQ} = m $，所以 $ S_{\text{四边形}BEMP} = 6m - m = 5m $。因为 $ BE = 2EC $，$ CF = 2AF $，所以 $ S_{\triangle BQE} = 2S_{\triangle CEQ} $，$ S_{\triangle CQF} = 2S_{\triangle AFQ} = 2m $，所以 $ S_{\triangle BQC} = 6m + 8m - 2m = 12m $，所以 $ S_{\triangle BQE} = 12m \times \frac{2}{3} = 8m $，所以 $ S_{\triangle PQM} = 8m - 5m = 3m = 1 $，所以 $ m = \frac{1}{3} $。所以 $ S_{\triangle ABC} = m + 6m + 8m + 6m = 21m = 21 \times \frac{1}{3} = 7 $。