《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

11. 新趋势 跨学科融合 (2024·唐山模拟)如图,在平面直角坐标系中,放置一平面镜AB,其中点A,B的坐标分别为(4,1),(4,5),从点C(-1,0)发射光线,其图象对应的函数表达式为$y= mx+n(m≠0,x≥-1)$.
(1)点D为平面镜的中点,若光线恰好经过点D,求CD所在直线的表达式;
(2)若入射光线$y= mx+n(m≠0,x≥-1)$与平面镜AB有公共点,求n的取值范围;
(3)规定横坐标与纵坐标均为整数的点是整点,光线$y= mx+n(m≠0,x≥-1)$经过镜面反射后,反射光线与y轴相交于点E,直接写出点E是整点的个数.

答案：

(1)
∵点A,B的坐标分别为(4,1),(4,5),点D为平面镜的中点,
∴D(4,3).将C,D坐标分别代入y = mx + n中,得$\begin{cases}4m + n = 3\\-m + n = 0\end{cases}$,解得$\begin{cases}m = \frac{3}{5}\\n = \frac{3}{5}\end{cases}$,
∴CD所在直线的表达式为y = $\frac{3}{5}$x + $\frac{3}{5}$.
(2)当入射光线y = mx + n(m≠0,x≥ - 1)经过C(-1,0),A(4,1)时,有$\begin{cases}4m + n = 1\\-m + n = 0\end{cases}$,解得$\begin{cases}m = \frac{1}{5}\\n = \frac{1}{5}\end{cases}$;当入射光线y = mx + n(m≠0,x≥ - 1)经过C(-1,0),B(4,5)时,有$\begin{cases}4m + n = 5\\-m + n = 0\end{cases}$,解得$\begin{cases}m = 1\\n = 1\end{cases}$,
∴当入射光线y = mx + n(m≠0,x≥ - 1)与平面镜AB有公共点时,n的取值范围为$\frac{1}{5}$≤n≤1.
(3)整点E有8个. 解析:如图,作出点C关于AB的对称点C',则C'(9,0),作直线AC',BC'分别交y轴于E₁,E₂,易得直线BC'的表达式为y = -x + 9,直线AC'的表达式为y = $\frac{1}{5}$x + $\frac{9}{5}$.
∵反射光线与y轴相交于点E,
∴点E纵坐标的取值范围为$\frac{9}{5}$≤n≤9,
∴整点E的纵坐标可以取2,3,4,5,6,7,8,9,共8个.

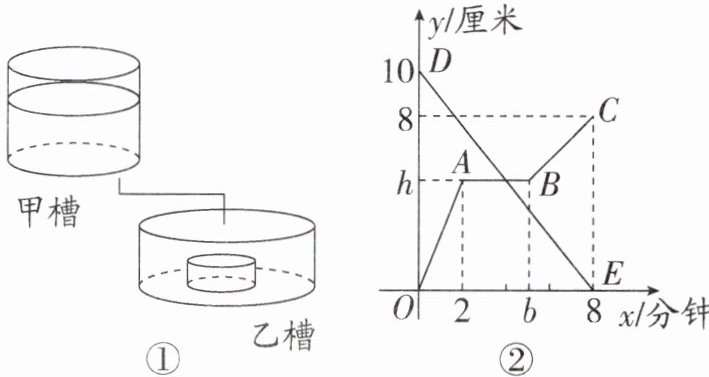
12. 新考法 如图①是甲、乙两个圆柱形水槽,一个圆柱形的空玻璃杯放置在乙槽中(空玻璃杯的厚度忽略不计).将甲槽的水匀速注入乙槽的空玻璃杯中,甲槽内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图②线段DE所示,乙槽(包括空玻璃杯)内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图②折线O-A-B-C所示.记甲槽底面积为$S_{1}$,乙槽底面积为$S_{2}$.则:
(1)甲槽开始注水时的水位为______厘米;
(2)$S_{1}:S_{2}= $______;
(3)$\frac {h}{b}= $______.

答案：
(1)10
(2)4:5　解析:由题意可得，甲槽最高水位是10厘米,乙槽最高水位是8厘米,
∴10S₁ = 8S₂,S₁:S₂ = 4:5.
(3)1　解析:由题图②可知，乙槽的空玻璃杯的高度是h厘米，设yDE = kx + b(x＞0),代入D,E两点,得$\begin{cases}b = 10\\8k + b = 0\end{cases}$,解得$\begin{cases}k = -\frac{5}{4}\\b = 10\end{cases}$,yDE = -$\frac{5}{4}$x + 10,令x = b,则y = $\frac{40 - 5b}{4}$,
∴b分钟,甲槽水位下降$\frac{5b}{4}$厘米,甲槽向乙槽注入的水的体积为$\frac{5b}{4}$S₁立方厘米,
∴hS₂ = $\frac{5b}{4}$S₁.
∵S₁:S₂ = 4:5,
∴$\frac{h}{b}$ = 1.

13. (齐齐哈尔中考)在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分钟)之间的函数关系如图所示,请结合图象解答下列问题:
(1)请写出甲的骑行速度为______米/分,点M的坐标为______;
(2)求甲返回时距A地的路程y与时间x之间的函数表达式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.

答案：
(1)240　(6,1200)　解析:由题意，得甲的骑行速度为$\frac{1020}{(\frac{21}{4} - 1)}$ = 240(米/分),240×(11 - 1)÷2 = 1200(米),点M的横坐标为(1200 - 1020)÷240 + $\frac{21}{4}$ = 6,则点M的坐标为(6,1200).
(2)设直线MN的表达式为y = kx + b(k≠0).
∵y = kx + b(k≠0)的图象过点M(6,1200),N(11,0),
∴$\begin{cases}6k + b = 1200\\11k + b = 0\end{cases}$,解得$\begin{cases}k = -240\\b = 2640\end{cases}$,
∴直线MN的表达式为y = -240x + 2640,即甲返回时距A地的路程y与时间x之间的函数表达式为y = -240x + 2640.
(3)4分钟或6分钟或8分钟. 解析:设甲返回A地之前,经过x分钟两人距C地的路程相等，可得乙的速度为1200÷20 = 60(米/分).
∵AB = 1200,AC = 1020,
∴BC = 1200 - 1020 = 180,
∴乙出发3分钟后到达C地，分5种情况:
①当0＜x≤3时,甲、乙在C地两侧,1020 - 240x = 180 - 60x,x = $\frac{14}{3}$＞3,此种情况不符合题意;
②当3＜x＜$\frac{21}{4}$ - 1时,甲、乙都在A,C之间,
∴1020 - 240x = 60x - 180,解得x = 4,符合题意;
③当$\frac{21}{4}$ - 1≤x≤$\frac{21}{4}$时,甲在C地不动,乙在A,C之间,不符合题意;
④当$\frac{21}{4}$＜x≤6时,甲在B,C之间,乙在A,C之间,
∴240(x - 1) - 1020 = 60x - 180,解得x = 6,符合题意;
⑤当x＞6时,甲在返回途中,当甲在B,C之间时,180 - [240(x - 1) - 1200] = 60x - 180,解得x = 6,此种情况不符合题意,当甲在A,C之间时,240(x - 1) - 1200 - 180 = 60x - 180,解得x = 8,符合题意.综上所述，在甲返回A地之前，经过4分钟或6分钟或8分钟时两人距C地的路程相等.