第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
1. 在如图所示的 $ 3 × 3 $ 网格中,$ \triangle ABC $ 是格点三角形(即顶点恰好是网格线的交点),请画出与 $ \triangle ABC $ 有一条公共边且全等(不含 $ \triangle ABC $)的所有格点三角形。
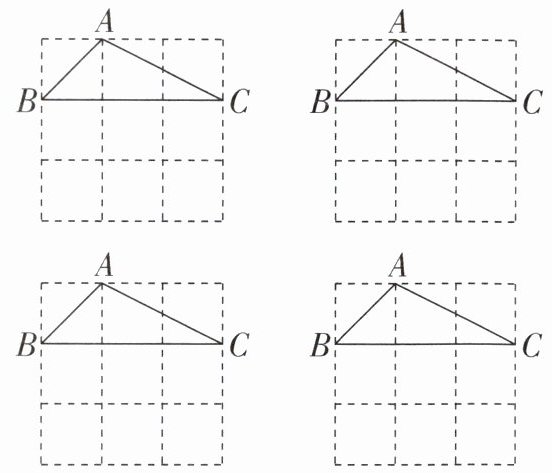

答案:
如图,$\triangle DBC$,$\triangle ECB$,$\triangle FCB$,$\triangle BAG$即为所求。

如图,$\triangle DBC$,$\triangle ECB$,$\triangle FCB$,$\triangle BAG$即为所求。

2. (2025·南京期末)如图,在正方形网格中,每个小正方形的顶点叫作格点。已知点 $ A $,$ B $,$ C $ 均在格点上。
(1)仅用无刻度的直尺在网格中画 $ AD // BC $,画 $ BE \perp AD $,垂足为 $ E $;
(2)比较大小:$ BE $______ $ AB $,理由是______;
(3)点 $ F $ 在射线 $ BC $ 上,请用无刻度的直尺和圆规作直线 $ FG // AB $(保留作图痕迹,不写作法)。
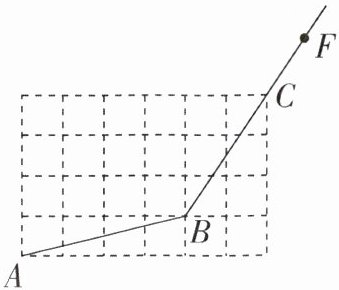
(1)仅用无刻度的直尺在网格中画 $ AD // BC $,画 $ BE \perp AD $,垂足为 $ E $;
(2)比较大小:$ BE $______ $ AB $,理由是______;
(3)点 $ F $ 在射线 $ BC $ 上,请用无刻度的直尺和圆规作直线 $ FG // AB $(保留作图痕迹,不写作法)。

答案:
(1) 如图①所示,$AD$,$BE$即为所求。

解析:如图②,取格点$G$,$H$,$I$,则格点$M$,$D$在格线$GH$上,设格线$IB$交$AD$于点$N$,由题意得$\angle AGD=\angle CIB=90^{\circ}$,$IN// GH$,$\therefore \angle ADG=\angle DNI$。$\because DG=BI=2$,$AG=CI=3$,$\therefore \triangle ADG\cong \triangle CBI$,$\therefore \angle ADG=\angle CBI=\angle DNB$,$\therefore AD// BC$。同理可得$\triangle ADG\cong \triangle MBH$,$\therefore \angle BMH=\angle GAD$。$\because \angle AGD=90^{\circ}$,$\therefore \angle ADG+\angle GAD=\angle ADG+\angle BMH=90^{\circ}$,$\therefore \angle MED=90^{\circ}$,$\therefore BE\perp AD$,$\therefore AD$,$BE$即为所求。

(2) < 垂线段最短
(3) 如图③,$FG$即为所求。

(1) 如图①所示,$AD$,$BE$即为所求。

解析:如图②,取格点$G$,$H$,$I$,则格点$M$,$D$在格线$GH$上,设格线$IB$交$AD$于点$N$,由题意得$\angle AGD=\angle CIB=90^{\circ}$,$IN// GH$,$\therefore \angle ADG=\angle DNI$。$\because DG=BI=2$,$AG=CI=3$,$\therefore \triangle ADG\cong \triangle CBI$,$\therefore \angle ADG=\angle CBI=\angle DNB$,$\therefore AD// BC$。同理可得$\triangle ADG\cong \triangle MBH$,$\therefore \angle BMH=\angle GAD$。$\because \angle AGD=90^{\circ}$,$\therefore \angle ADG+\angle GAD=\angle ADG+\angle BMH=90^{\circ}$,$\therefore \angle MED=90^{\circ}$,$\therefore BE\perp AD$,$\therefore AD$,$BE$即为所求。

(2) < 垂线段最短
(3) 如图③,$FG$即为所求。

3. (赤峰中考)如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^\circ $,且 $ AC = AD $。
(1)作 $ \angle BAC $ 的平分线,交 $ BC $ 于点 $ E $;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接 $ DE $,证明:$ AB \perp DE $。

(1)作 $ \angle BAC $ 的平分线,交 $ BC $ 于点 $ E $;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接 $ DE $,证明:$ AB \perp DE $。

答案:
(1) 如图,$AE$为$\angle BAC$的平分线。
(2) 如图,连接$DE$,由
(1)知$\angle CAE=\angle DAE$,在$\triangle ACE$和$\triangle ADE$中,$\left\{\begin{array}{l} AC=AD,\\ \angle CAE=\angle DAE,\\ AE=AE,\end{array}\right. $ $\therefore \triangle ACE\cong \triangle ADE(SAS)$,$\therefore \angle ACE=\angle ADE$。又$\because \angle ACB=90^{\circ}$,$\therefore \angle ADE=90^{\circ}$,$\therefore AB\perp DE$。

(1) 如图,$AE$为$\angle BAC$的平分线。
(2) 如图,连接$DE$,由
(1)知$\angle CAE=\angle DAE$,在$\triangle ACE$和$\triangle ADE$中,$\left\{\begin{array}{l} AC=AD,\\ \angle CAE=\angle DAE,\\ AE=AE,\end{array}\right. $ $\therefore \triangle ACE\cong \triangle ADE(SAS)$,$\therefore \angle ACE=\angle ADE$。又$\because \angle ACB=90^{\circ}$,$\therefore \angle ADE=90^{\circ}$,$\therefore AB\perp DE$。

4. 新趋势 项目式学习(2024·海安月考)通过“探索三角形全等的条件”的学习,大家知道“两边和它们的夹角分别相等的两个三角形全等”是一个基本事实,可以判定两个三角形全等;而满足条件“两边和其中一边所对的角分别相等”的两个三角形却不一定全等。下面请你来探究。
探究:已知:$ \triangle ABC $。
求作:$ \triangle DEF $,使 $ EF = BC $,$ \angle E = \angle B $,$ DF = AC $(即两边和其中一边所对的角分别相等)。
(1)实践与操作:请依据下面的步骤,用尺规完成作图过程。(保留作图痕迹)
①画 $ EF = BC $;②在线段 $ EF $ 的上方画 $ \angle E = \angle B $;③画 $ DF = AC $;④顺次连接相应顶点得所求三角形。
(2)观察与小结:观察你画的图形,你会发现满足条件的三角形有______个;其中三角形______(填三角形的名称)与 $ \triangle ABC $ 明显不全等,因此可得结论:______。
(3)猜想与验证:猜想是否存在满足“两边和其中一边所对的角分别相等”的两个三角形全等呢?存在与否,请举一例尺规作图验证(提示:按照探究中的已知先构造三角形,再根据求作要求尺规作图)。
(4)归纳与总结:用一句话归纳(3)。
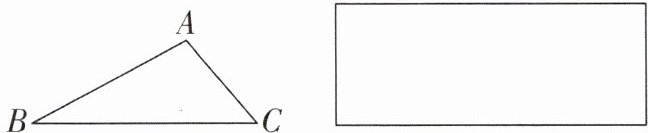
(实践与操作作图区)

(猜想与验证作图区)
电
探究:已知:$ \triangle ABC $。
求作:$ \triangle DEF $,使 $ EF = BC $,$ \angle E = \angle B $,$ DF = AC $(即两边和其中一边所对的角分别相等)。
(1)实践与操作:请依据下面的步骤,用尺规完成作图过程。(保留作图痕迹)
①画 $ EF = BC $;②在线段 $ EF $ 的上方画 $ \angle E = \angle B $;③画 $ DF = AC $;④顺次连接相应顶点得所求三角形。
(2)观察与小结:观察你画的图形,你会发现满足条件的三角形有______个;其中三角形______(填三角形的名称)与 $ \triangle ABC $ 明显不全等,因此可得结论:______。
(3)猜想与验证:猜想是否存在满足“两边和其中一边所对的角分别相等”的两个三角形全等呢?存在与否,请举一例尺规作图验证(提示:按照探究中的已知先构造三角形,再根据求作要求尺规作图)。
(4)归纳与总结:用一句话归纳(3)。

(实践与操作作图区)

(猜想与验证作图区)
电
答案:
(1) 作图如图①所示。

(2) 两 $D_{2}EF$ 两边和其中一边所对的角分别相等的两个三角形不一定全等
(3) 如图②,当$\angle ABC=90^{\circ}$时,按步骤作图,可得$\triangle DEF\cong \triangle ABC$。

如图③,当$\angle ABC>90^{\circ}$时,按步骤作图,也可得$\triangle DEF\cong \triangle ABC$。

(4) 两个三角形的两边和其中一边所对的角分别相等,且该角为直角或钝角时,这两个三角形全等(合理即可)
(1) 作图如图①所示。

(2) 两 $D_{2}EF$ 两边和其中一边所对的角分别相等的两个三角形不一定全等
(3) 如图②,当$\angle ABC=90^{\circ}$时,按步骤作图,可得$\triangle DEF\cong \triangle ABC$。

如图③,当$\angle ABC>90^{\circ}$时,按步骤作图,也可得$\triangle DEF\cong \triangle ABC$。

(4) 两个三角形的两边和其中一边所对的角分别相等,且该角为直角或钝角时,这两个三角形全等(合理即可)
查看更多完整答案,请扫码查看


