第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
新趋势 项目式学习 根据以下素材,回答问题:
素材1:在魏晋时期,数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法。所谓割圆术,即通过圆内接正多边形细割圆,并使正多边形的周长与面积无限接近圆的周长与面积,进而求得较为精确的圆周率。刘徽形容“割圆术”:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。”
素材2:“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据:设实数x的不足近似值和过剩近似值分别为$\frac {b}{a}和\frac {d}{c}$(即有$\frac {b}{a}\lt x<\frac {d}{c}$,其中a,b,c,d为正整数),则$\frac {b+d}{a+c}$是x的更为精确的近似值。例如:已知$\frac {7}{5}<\sqrt {2}<\frac {3}{2}$,则利用一次“调日法”后可得到$\sqrt {2}的一个更为精确的近似分数为\frac {7+3}{5+2}= \frac {10}{7}$;由于$\frac {10}{7}>\sqrt {2}$,可得$\frac {7}{5}<\sqrt {2}<\frac {10}{7}$,之后可以再次使用“调日法”得到$\sqrt {2}$的更为精确的近似分数。
素材3:在日常生活中,我们也可以估计π的值,如通过卷尺量得一个圆形平台直径为2m,周长为6.3m,则可利用圆的周长公式估计π的值。
任务1:(1)①如图①,已知圆的内接正六边形可分为六个全等的等边三角形,每个三角形的边长均为圆的半径R。若将圆内接正六边形的周长等同于圆的周长,则可得π的估计值为____。
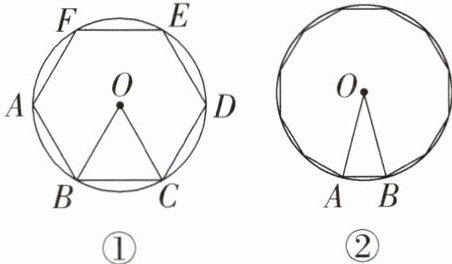
②如图②,已知圆的内接正十二边形可分为十二个全等的等腰三角形,且等腰三角形的顶角为30°。若将圆内接正十二边形的面积等同于圆的面积,则可得π的估计值为____。
任务2:(2)约公元前240年,阿基米德算得$3\frac {10}{71}<π<3\frac {1}{7}$,已知$\frac {245}{78}<π$,请在此基础上使用两次“调日法”得到π的更为精确的近似分数。
任务3:(3)①利用素材3,可估计π的值为____。
②已知球的体积公式是$V= \frac {4}{3}πR^{3}$,其中R是球的半径。小华量得一个球形空心容器的半径为60cm(忽略容器厚度),往其中注入$0.9m^{3}$的水可将该容器注满,则可估计π的值为____。
素材1:在魏晋时期,数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法。所谓割圆术,即通过圆内接正多边形细割圆,并使正多边形的周长与面积无限接近圆的周长与面积,进而求得较为精确的圆周率。刘徽形容“割圆术”:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。”
素材2:“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据:设实数x的不足近似值和过剩近似值分别为$\frac {b}{a}和\frac {d}{c}$(即有$\frac {b}{a}\lt x<\frac {d}{c}$,其中a,b,c,d为正整数),则$\frac {b+d}{a+c}$是x的更为精确的近似值。例如:已知$\frac {7}{5}<\sqrt {2}<\frac {3}{2}$,则利用一次“调日法”后可得到$\sqrt {2}的一个更为精确的近似分数为\frac {7+3}{5+2}= \frac {10}{7}$;由于$\frac {10}{7}>\sqrt {2}$,可得$\frac {7}{5}<\sqrt {2}<\frac {10}{7}$,之后可以再次使用“调日法”得到$\sqrt {2}$的更为精确的近似分数。
素材3:在日常生活中,我们也可以估计π的值,如通过卷尺量得一个圆形平台直径为2m,周长为6.3m,则可利用圆的周长公式估计π的值。
任务1:(1)①如图①,已知圆的内接正六边形可分为六个全等的等边三角形,每个三角形的边长均为圆的半径R。若将圆内接正六边形的周长等同于圆的周长,则可得π的估计值为____。
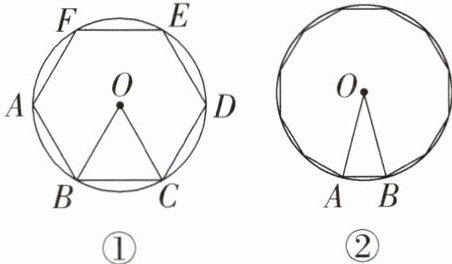
②如图②,已知圆的内接正十二边形可分为十二个全等的等腰三角形,且等腰三角形的顶角为30°。若将圆内接正十二边形的面积等同于圆的面积,则可得π的估计值为____。
任务2:(2)约公元前240年,阿基米德算得$3\frac {10}{71}<π<3\frac {1}{7}$,已知$\frac {245}{78}<π$,请在此基础上使用两次“调日法”得到π的更为精确的近似分数。
任务3:(3)①利用素材3,可估计π的值为____。
②已知球的体积公式是$V= \frac {4}{3}πR^{3}$,其中R是球的半径。小华量得一个球形空心容器的半径为60cm(忽略容器厚度),往其中注入$0.9m^{3}$的水可将该容器注满,则可估计π的值为____。
答案:
(1)①3 解析:此时圆内接正六边形的周长为 6R,由 $2\pi R = 6R$ 可得 $\pi$ 的估计值为 3.
②3 解析:如图,AB 是正十二边形的一条边,点 O 是正十二边形的中心,设圆 O 的半径为 R,过 A 作 $AM \perp OB$ 于点 M,由题意可得 $\angle AOB = 30^\circ$, $\therefore AM = \frac{1}{2}OA = \frac{1}{2}R$, $\therefore S_{\triangle AOB} = \frac{1}{2}OB \cdot AM = \frac{1}{2} \times R \times \frac{1}{2}R = \frac{1}{4}R^2$, $\therefore$ 正十二边形的面积为 $12 \times \frac{1}{4}R^2 = 3R^2$, $\therefore 3R^2 = R^2 \times \pi$, $\therefore \pi = 3$, $\therefore \pi$ 的近似值为 3.

(2) $\because 3\frac{10}{71} < \pi < 3\frac{1}{7}$, 即 $\frac{223}{71} < \pi < \frac{22}{7}$, $\therefore$ 使用一次“调日法”后可得到 $\pi$ 的一个更为精确的近似分数为 $\frac{223 + 22}{71 + 7} = \frac{245}{78}$. $\because \frac{245}{78} < \pi$, 可得 $\frac{245}{78} < \pi < \frac{22}{7}$, 之后可以再次使用“调日法”得到 $\pi$ 的更为精确的近似分数为 $\frac{245 + 22}{78 + 7} = \frac{267}{85}$, 故在此基础上使用两次“调日法”得到 $\pi$ 的更为精确的近似分数为 $\frac{267}{85}$.
(3)①3.15
②3.125 解析:60 cm = 0.6 m, 则 $\frac{4}{3}\pi \times (0.6)^3 = 0.9$, 可得 $\pi = \frac{0.9}{0.288} = 3.125$.
(1)①3 解析:此时圆内接正六边形的周长为 6R,由 $2\pi R = 6R$ 可得 $\pi$ 的估计值为 3.
②3 解析:如图,AB 是正十二边形的一条边,点 O 是正十二边形的中心,设圆 O 的半径为 R,过 A 作 $AM \perp OB$ 于点 M,由题意可得 $\angle AOB = 30^\circ$, $\therefore AM = \frac{1}{2}OA = \frac{1}{2}R$, $\therefore S_{\triangle AOB} = \frac{1}{2}OB \cdot AM = \frac{1}{2} \times R \times \frac{1}{2}R = \frac{1}{4}R^2$, $\therefore$ 正十二边形的面积为 $12 \times \frac{1}{4}R^2 = 3R^2$, $\therefore 3R^2 = R^2 \times \pi$, $\therefore \pi = 3$, $\therefore \pi$ 的近似值为 3.

(2) $\because 3\frac{10}{71} < \pi < 3\frac{1}{7}$, 即 $\frac{223}{71} < \pi < \frac{22}{7}$, $\therefore$ 使用一次“调日法”后可得到 $\pi$ 的一个更为精确的近似分数为 $\frac{223 + 22}{71 + 7} = \frac{245}{78}$. $\because \frac{245}{78} < \pi$, 可得 $\frac{245}{78} < \pi < \frac{22}{7}$, 之后可以再次使用“调日法”得到 $\pi$ 的更为精确的近似分数为 $\frac{245 + 22}{78 + 7} = \frac{267}{85}$, 故在此基础上使用两次“调日法”得到 $\pi$ 的更为精确的近似分数为 $\frac{267}{85}$.
(3)①3.15
②3.125 解析:60 cm = 0.6 m, 则 $\frac{4}{3}\pi \times (0.6)^3 = 0.9$, 可得 $\pi = \frac{0.9}{0.288} = 3.125$.
查看更多完整答案,请扫码查看


