《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

6. (邵阳中考) 小明参加 $ 100 \mathrm { m } $ 短跑训练, 2018 年 1 - 4 月的训练成绩如下表所示:

体育老师夸奖小明是“田径天才”, 请你预测小明 5 年 (60 个月) 后 $ 100 \mathrm { m } $ 短跑的成绩为 (温馨提示: 目前 $ 100 \mathrm { m } $ 短跑世界记录为 9 秒 58 ) ()
A. $ 14.8 \mathrm { s } $
B. $ 3.8 \mathrm { s } $
C. $ 3 \mathrm { s } $
D. 预测结果不可靠

答案： D 解析:若短跑的成绩与月份满足一次函数关系，计算可得 5 年后 100 m 短跑的成绩为 3.8 s，这与事实不符，故短跑的成绩与月份不满足一次函数关系，无法预测，故选 D。

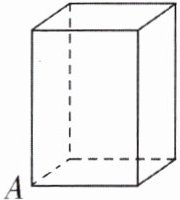
7. (绍兴中考) 实验室里有一个水平放置的长方体容器, 从内部量得它的高是 $ 15 \mathrm { cm } $, 底面的长是 $ 30 \mathrm { cm } $, 宽是 $ 20 \mathrm { cm } $, 容器内的水深为 $ x \mathrm { cm } $. 现往容器内放入如图的长方体实心铁块 (铁块一面平放在容器底面), 过顶点 $ A $ 的三条棱的长分别为 $ 10 \mathrm { cm } $, $ 10 \mathrm { cm } $, $ y \mathrm { cm } ( y \leq 15 ) $, 当铁块的顶部高出水面 $ 2 \mathrm { cm } $ 时, $ x $, $ y $ 满足的表达式是______.

答案： $ y = \frac{6x + 10}{5}\left(0 ＜ x ≤ \frac{65}{6}\right) $ 或 $ y = \frac{120 - 15x}{2}(6 ≤ x ＜ 8) $
解析:① 当长方体实心铁块的棱长为 10 cm 和 $ y $ cm 的那一面平放在长方体的容器底面时，则铁块浸在水中的高度为 8 cm，此时，水位上升了 $ (8 - x) \mathrm{cm}(x ＜ 8) $，铁块浸在水中的体积为 $ 10×8×y = 80y(\mathrm{cm}^3) $，
∴ $ 80y = 30×20×(8 - x) $，
∴ $ y = \frac{120 - 15x}{2} $。
∵ $ y ≤ 15 $，
∴ $ x ≥ 6 $，即 $ y = \frac{120 - 15x}{2}(6 ≤ x ＜ 8) $。② 当长方体实心铁块的棱长为 10 cm 和 10 cm 的那一面平放在长方体的容器底面时，同①的方法，得 $ y = \frac{6x + 10}{5}\left(0 ＜ x ≤ \frac{65}{6}\right) $。

8. (2023·呼和浩特中考) 学校通过劳动教育促进学生树德、增智、强体、育美全面发展, 计划组织八年级学生到“开心”农场开展劳动实践活动. 到达农场后分组进行劳动, 若每位老师带 38 名学生, 则还剩 6 名学生没老师带; 若每位老师带 40 名学生, 则有一位老师少带 6 名学生. 劳动实践结束后, 学校在租车总费用 2300 元的限额内, 租用汽车送师生返校, 每辆车上至少要有 1 名老师. 现有甲、乙两种大型客车, 它们的载客量和租金如表所示:

(1) 参加本次实践活动的老师和学生各有多少名?
(2) 租车返校时, 既要保证所有师生都有车坐, 又要保证每辆车上至少有 1 名老师, 则共需租车______辆.
(3) 学校共有几种租车方案? 最少租车费用是多少?

答案：
(1) 设老师有 $ x $ 名，学生有 $ y $ 名，根据题意，得 $ \begin{cases} 38x + 6 = y, \\ 40x - 6 = y, \end{cases} $ 解得 $ \begin{cases} x = 6, \\ y = 234. \end{cases} $ 答:老师有 6 名，学生有 234 名。
(2) 6 解析:
∵ 每辆车上至少有 1 名老师，
∴ 汽车总数不能大于 6 辆。
∵ 要保证 240 名师生都有车坐，
∴ 汽车总数不能少于 $ \frac{240}{45} $ (取整数 6) 辆。综合可知汽车总数为 6 辆。
(3) 设租用甲型客车 $ m $ 辆，则租车费用 $ w $ (元) 是 $ m $ 的函数，即 $ w = 400m + 280(6 - m) $，整理得 $ w = 120m + 1680 $。
∵ 学校在租车总费用 2300 元的限额内，租用汽车送师生返校，
∴ $ 120m + 1680 ≤ 2300 $，
∴ $ m ≤ \frac{31}{6} $，即 $ m ≤ 5 $。要保证 240 人都有车坐，
∴ $ 45m + 30(6 - m) ≥ 240 $，解得 $ m ≥ 4 $，
∴ 有两种租车方案:方案一:租 4 辆甲型客车，2 辆乙型客车；方案二:租 5 辆甲型客车，1 辆乙型客车。
∵ $ w $ 随 $ m $ 的增大而增大，
∴ 当 $ m = 4 $ 时，$ w $ 最小，$ w = 120×4 + 1680 = 2160 $。答:学校共有两种租车方案，最少租车费用为 2160 元。

9. (2025·安庆校级月考) 某商场准备购进甲、乙两种服装进行销售. 甲种服装每件进价 160 元, 售价 210 元; 乙种服装每件进价 120 元, 售价 150 元. 现计划购进两种服装共 100 件, 其中甲种服装不少于 60 件. 设购进甲种服装 $ x $ 件, 两种服装全部售完, 商场获利 $ y $ 元.
(1) 求 $ y $ 与 $ x $ 之间的函数表达式;
(2) 若购进 100 件服装的总费用不超过 15000 元, 求最大利润为多少元;
(3) 在 (2) 的条件下, 该服装店对甲种服装以每件优惠 $ a ( 0 ＜ a ＜ 20 ) $ 元的价格进行优惠促销活动, 乙种服装每件进价减少 $ b $ 元, 售价不变, 且 $ a - b = 4 $, 若最大利润为 4000 元, 求 $ a $ 的值.

答案：
(1) $ y = (210 - 160)x + (150 - 120)(100 - x) = 20x + 3000 $。
(2) 由题意得 $ \begin{cases} x ≥ 60, \\ 160x + 120×(100 - x) ≤ 15000, \end{cases} $
∴ $ 60 ≤ x ≤ 75 $，
∵ $ y = 20x + 3000 $ 中 $ k = 20 ＞ 0 $，
∴ $ y $ 随 $ x $ 的增大而增大，
∴ 当 $ x = 75 $ 时，$ y_{\text{最大}} = 20×75 + 3000 = 4500 $，即最大利润为 4500 元。
(3)
∵ $ a - b = 4 $，
∴ $ b = a - 4 $。由题意得 $ y = (210 - 160 - a)x + (150 - 120 + b)(100 - x) = (50 - a)x + (30 + b)×100 - (30 + b)x = (24 - 2a)x + 100a + 2600 $。
∵ $ 60 ≤ x ≤ 75 $，$ 0 ＜ a ＜ 20 $，
∴ 当 $ 0 ＜ a ＜ 12 $ 时，$ 24 - 2a ＞ 0 $，
∴ $ y $ 随 $ x $ 的增大而增大，
∴ 当 $ x = 75 $ 时，$ y_{\text{最大}} = (24 - 2a)×75 + 100a + 2600 = 4000 $，
∴ $ a = 8 $，符合题意。当 $ a = 12 $ 时，$ y = 100×12 + 2600 = 3800 ≠ 4000 $，不符合题意。当 $ 12 ＜ a ＜ 20 $ 时，$ 24 - 2a ＜ 0 $，$ y $ 随 $ x $ 的增大而减小，
∴ 当 $ x = 60 $ 时，$ y_{\text{最大}} = (24 - 2a)×60 + 100a + 2600 = 4000 $，
∴ $ a = 2 $，不符合题意，舍去。综上，$ a = 8 $。