《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

1. (2024·自贡中考改编)在 $ 0,-2,\sqrt{3},\pi $ 四个数中,最大的数是 ()
A. -2
B. 0
C. $ \pi $
D. $ \sqrt{3} $

答案： C

2. 下列各组数中互为相反数的是 ()
A. 5 和 $ \sqrt{(-5)^2} $
B. $ -|-2| $ 和 $ \sqrt[3]{-8} $
C. $ -\sqrt[3]{8} $ 和 $ \sqrt[3]{-8} $
D. $ -(-2) $ 和 $ -\sqrt{(-2)^2} $

答案： D

3. (2024·烟台期末)用科学计算器进行计算,按键顺序依次为 $ \sqrt{\square} $ $ 1 $ $ 0 $ $ - $ $ 1 $ $ = $,则计算器显示结果与下列各数最接近的一个是 ()
A. 1.2
B. 2.0
C. 2.2
D. 2.3

答案： C

4. (1)(吉林中考)实数 $ -\sqrt{2} $ 的相反数是____;
(2)$ -\sqrt{3} $ 的绝对值的相反数是____;
(3)$ 1-\sqrt{2} $ 的绝对值的相反数是____.

答案：
(1)$\sqrt {2}$
(2)$-\sqrt {3}$
(3)$1-\sqrt {2}$

5. 新趋势 开放性试题 (2024·深圳中考)如图所示,四边形 $ ABCD,DEFG,GHIJ $ 均为正方形,且 $ S_{\text{正方形}ABCD}= 10,S_{\text{正方形}GHIJ}= 1 $,则正方形 $ DEFG $ 的边长可以是____.(写出一个答案即可)

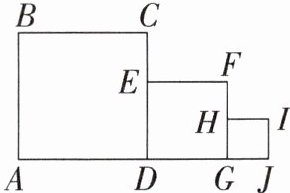
答案： 2(答案不唯一)

6. 比较下列各组数的大小(填“＞”“＜”或“=”)：
(1)(2024·山西中考)$ \sqrt{6} $____2;
(2)$ -\sqrt{2} $____$ -\sqrt{3} $;
(3)(临沂中考)$ \frac{\sqrt{3}}{3} $____$ \frac{\sqrt{2}}{2} $;
(4)$ \sqrt{5}-3 $____$ \frac{\sqrt{5}-2}{2} $.

答案：
(1)＞
(2)＞
(3)＜
(4)＜

7. 计算:
(1)$ |\sqrt{3}-1|-(-\sqrt{3})^2-12 × \left(-\frac{1}{3}\right) $;
(2)$ \sqrt{5}+|2-\sqrt{5}|-\sqrt[3]{-64}+\sqrt{(-2)^2} $.

答案：
(1)原式$=\sqrt {3}-1-3+4=\sqrt {3}$.
(2)原式$=\sqrt {5}+(\sqrt {5}-2)-(-4)+2=\sqrt {5}+\sqrt {5}-2+4+2=2\sqrt {5}+4$.

8. 如图是一个数值转换机的示意图,请从方框内的4个数中选择一个有理数和一个无理数,并计算输出结果.

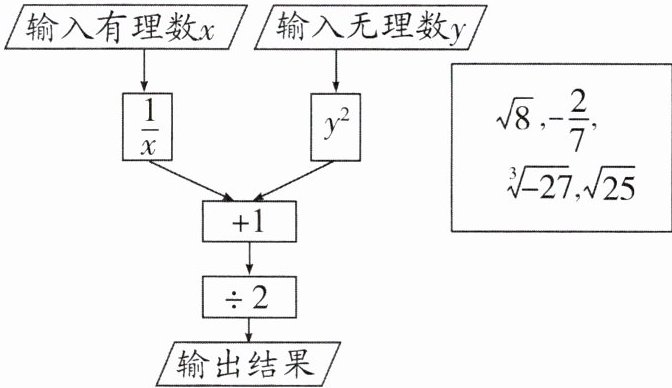
答案： 答案不唯一,选一个有理数和一个无理数即可.
![img alt=8]

9. (临沂中考改编)满足 $ m＞|\sqrt{10}-1| $ 的整数 $ m $ 的值最小是 ()
A. 5
B. 4
C. 3
D. 2

答案： C 解析:$\because 3＜\sqrt {10}＜4,\therefore 2＜\sqrt {10}-1＜3.\because |\sqrt {10}-1|=\sqrt {10}-1,m＞|$ $\sqrt {10}-1|,\therefore m≥3$,
∴ 整数 m 的值最小是 3,故选 C.

10. (绵阳中考)正整数 $ a,b $ 分别满足 $ \sqrt[3]{53}＜a＜\sqrt[3]{98},\sqrt{2}＜b＜\sqrt{7} $,则 $ b^a= $ ()
A. 4
B. 8
C. 9
D. 16

答案： D 解析:$\because \sqrt [3]{27}＜\sqrt [3]{53}＜a＜\sqrt [3]{98}＜\sqrt [3]{125},\sqrt {1}＜\sqrt {2}＜b＜\sqrt {7}＜\sqrt {9}$,a,b 为正整数,$\therefore a=4,b=2,\therefore b^{a}=2^{4}=16$.故选 D.