《2025年学霸甘肃少年儿童出版社八年级数学上册苏科版》

1. (2023·湘西州中考)在平面直角坐标系中,已知点$P(a,1)与点Q(2,b)$关于x轴对称,则$a+b= $ ()
A. -1
B. -3
C. 1
D. 3

答案： C

2. 点$P(a+2,2a-5)$关于y轴的对称点在第二象限,则a的取值范围是 ()
A. $a＜-2$
B. $-2＜a＜\frac{5}{2}$
C. $-\frac{5}{2}＜a＜2$
D. $a＞\frac{5}{2}$

答案： D

3. 在平面直角坐标系中,点P的坐标为$(-2,1)$.
(1)作点P关于x轴的对称点,得到点$P'$,再作点$P'$关于y轴的对称点,得到点$P''$,则点$P'$的坐标是____,点$P''$的坐标是____;
(2)点P关于原点对称的点的坐标是____.

答案：
(1)$(-2,-1)$ $(2,-1)$
(2)$(2,-1)$

4. (2025·济南校级月考)剪纸艺术是最古老的中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,点E的坐标为$(-2,-n)$,其关于y轴对称的点F的坐标为$(2,-m+1)$,则$(n-m)^{2025}= $____.

答案： -1

5. (2025·北京期末)如图,在$3×3$的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是点____.

答案： D

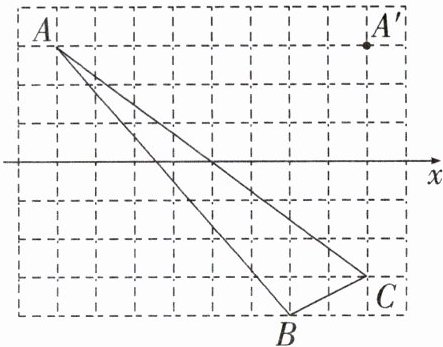
6. 如图是一个不完整的平面直角坐标系,小正方形的边长均为1,$△ABC与△A'B'C'$关于y轴对称,点$A'$是点A的对称点.
(1)请在图中画出缺少的y轴,并写出点B的坐标;
(2)请在图中画出$△A'B'C'$,并写出点$C'$的坐标;
(3)在上述的基础上,连接$AA',CC'$,判断线段$AA'与线段CC'$是否关于x轴对称.

答案：

(1)如图,y轴为所求,B(2,-4).
(2)如图,$△A'B'C'$为所求,$C'(-4,-3).$
(3)如图,线段$AA'$与线段$CC'$关于x轴对称.

7. 在平面直角坐标系中,$A(a,b)(b≠0),B(m,n)$.若$a-m= 4,b+n= 0$,则下列结论正确的是 ()
A. 把点A向左平移4个单位长度后,与点B关于x轴对称
B. 把点A向右平移4个单位长度后,与点B关于x轴对称
C. 把点A向左平移4个单位长度后,与点B关于y轴对称
D. 把点A向右平移4个单位长度后,与点B关于y轴对称

答案： A 解析:$\because a-m=4,\therefore a-4=m$.又$\because b+n=0(b≠0),\therefore b=-n$,
∴ 把点A向左平移4个单位长度后,与点B关于x轴对称.故选A.

8. 已知点$B(1,0)与点B'$关于y轴对称,直线m过点$B(1,0)$且与y轴平行,点$C(4,2)与点C'$关于直线m对称,则$B'C'$的长为____.

答案：
$\sqrt {5}$ 解析:
∵ 点$B(1,0)$与点$B'$关于y轴对称,
∴ 点$B'(-1,0)$.
∵ 直线m过点$B(1,0)$且与y轴平行,
∴ 作直线m如图所示.
∵ 点$C(4,2)$与点$C'$关于直线m对称,
∴ 点$C'(-2,2),\therefore B'C'=\sqrt {1^{2}+2^{2}}=\sqrt {5}.$