(1)在同一幅地图上,实际距离和图上距离成( )比例。
答案:
(1)正
(1)正
(2)时间、路程和速度三者之间,当( )一定时,( )和( )成反比例;当( )一定时,( )和( )成正比例。
答案:
(2)路程 时间 速度 速度(或时间) 路程 时间(或速度)
(2)路程 时间 速度 速度(或时间) 路程 时间(或速度)
(3)把6g的盐放入54g的水中配制成盐水,盐和盐水质量的比值是( ),用10g盐能配制成相同浓度的盐水( )g,需要水( )g。
答案:
(3)$\frac{1}{10}$ 100 90
(3)$\frac{1}{10}$ 100 90
(4)如右图,两个正方形中涂色部分的面积比是2:1,空白部分甲和乙的面积比是( )。若空白部分甲的面积是2.4dm²,则两个正方形的面积之和是( )dm²。

答案:
(4)6:1 4
(4)6:1 4
(1)下面各选项中的两个量,不成比例的是( )。
A. 正方形的边长和面积
B. 三角形的高一定,它的面积和底
C. 总价一定,单价和数量
A. 正方形的边长和面积
B. 三角形的高一定,它的面积和底
C. 总价一定,单价和数量
答案:
(1)A
(1)A
(2)下列关系式中,能表示a和b成反比例的是( )。(a和b均不为0)
A. $a + b = 5$ B. $\frac{a}{b}=5$ C. $\frac{a}{3}=\frac{5}{b}$
A. $a + b = 5$ B. $\frac{a}{b}=5$ C. $\frac{a}{3}=\frac{5}{b}$
答案:
(2)C
(2)C
(3)在同时同地测得的竿高和影长( )。
A. 成正比例 B. 成反比例 C. 不成比例
A. 成正比例 B. 成反比例 C. 不成比例
答案:
(3)A
(3)A
3. 某造纸厂的生产情况如下表。
(1)将表格补充完整。
(2)表中的两个量成正比例吗?为什么?
(3)根据表中数据,生产560t纸大约要用多少天?

(1)将表格补充完整。
(2)表中的两个量成正比例吗?为什么?
(3)根据表中数据,生产560t纸大约要用多少天?

答案:
(1)填表如下:

(2)因为 $\frac{70}{1}=\frac{140}{2}=\frac{210}{3}\cdots$ ,生产量与时间的比值恒为 70,所以表中的两个量成正比例。
(3)560÷70 = 8(天)
答:生产 560t 纸大约要用 8 天。
(1)填表如下:

(2)因为 $\frac{70}{1}=\frac{140}{2}=\frac{210}{3}\cdots$ ,生产量与时间的比值恒为 70,所以表中的两个量成正比例。
(3)560÷70 = 8(天)
答:生产 560t 纸大约要用 8 天。
4. 甲、乙两台机器的工作时间和耗电量如下表。
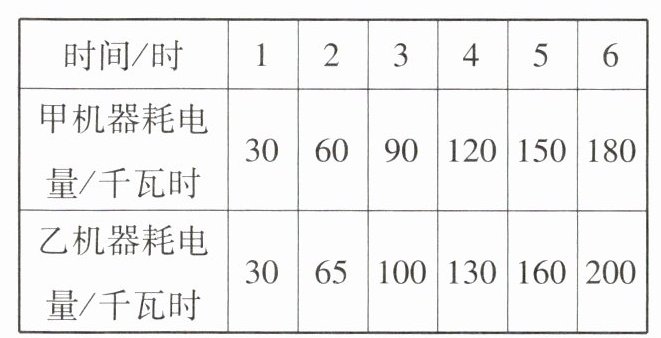
(1)根据表中的数据,在下图中描出每一组工作时间与耗电量所对应的点,再把它们按顺序连接起来。
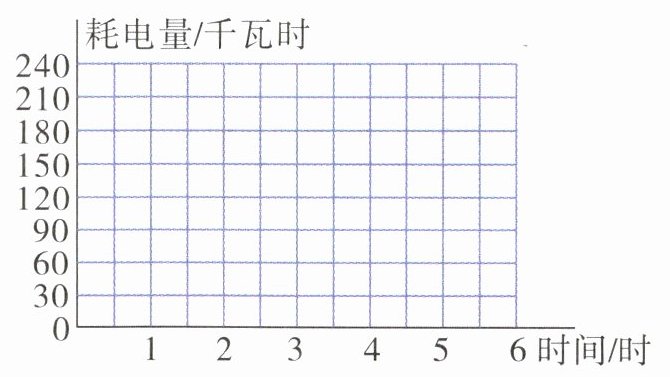
(2)根据画出的图象可得( )机器的工作时间和耗电量成正比例。
(3)根据画出的图象,工作2.5时,甲机器的耗电量大约是( )千瓦时,乙机器的耗电量大约是( )千瓦时。

(1)根据表中的数据,在下图中描出每一组工作时间与耗电量所对应的点,再把它们按顺序连接起来。

(2)根据画出的图象可得( )机器的工作时间和耗电量成正比例。
(3)根据画出的图象,工作2.5时,甲机器的耗电量大约是( )千瓦时,乙机器的耗电量大约是( )千瓦时。
答案:
(1)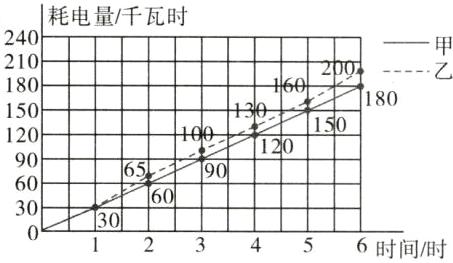
(2)甲
(3)75 82.5(合理即可)
(1)

(2)甲
(3)75 82.5(合理即可)
查看更多完整答案,请扫码查看


