《2025年高效课堂新疆青少年出版社六年级数学下册北师大版》

1. (河源期末真题)填空题。
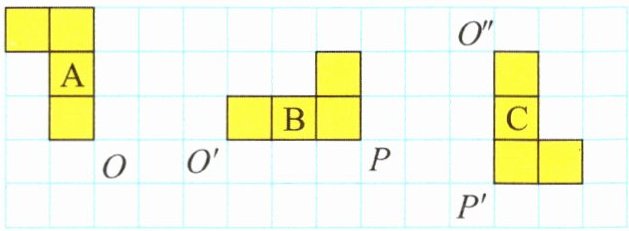
(1)图形B可看作由图形A绕点O顺时针旋转(　　　)，又向(　　　)平移(　　　)格得到的。
(2)图形C可看作由图形B绕点P顺时针旋转(　　　)，向下平移(　　　)格，又向(　　　)平移(　　　)格得到的。

答案：
(1)$90^{\circ}$ 右 3
(2)$90^{\circ}$ 1 右 3

(1)旋转和平移的共同点是(　　　)。
A. 都是沿一定的方向移动一定的距离
B. 都不改变图形的形状和大小
C. 对应线段都互相平行

答案：
(1)B

(2)下面各组图形中，可以通过平移得到另一个图形的是(　　　)。

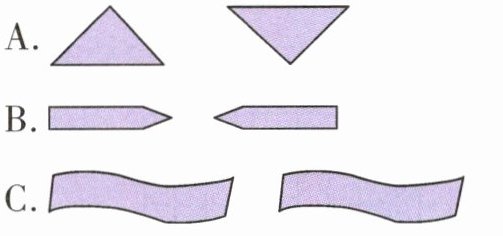
答案：
(2)C

(3)如图，平行四边形ABCD绕点A逆时针旋转90°，再向左平移(　　　)格就得到平行四边形A'B'C'D'。
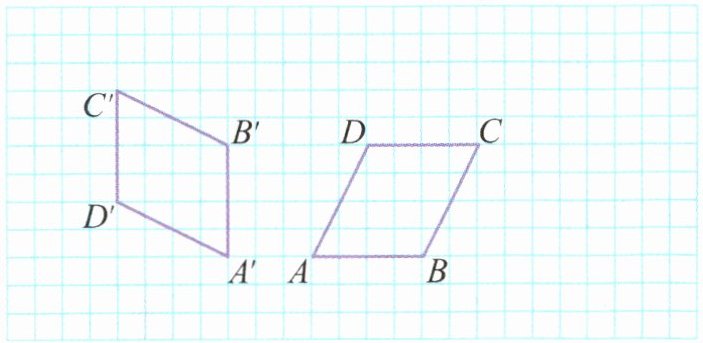
A. 2
B. 3
C. 5

答案：
(3)B

3. 操作题。
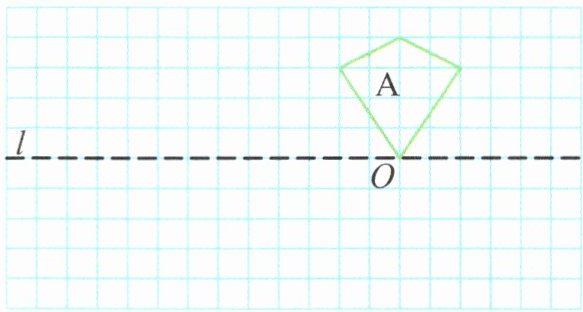
(1)以直线l为对称轴作图形A的轴对称图形，得到图形B。
(2)将图形B向左平移6格，得到图形C。
(3)将图形B绕点O顺时针旋转90°，得到图形D。

答案：

(1)
(2)
(3)

4. 观察下图，这两个三角形如何运动能拼成一个正方形?

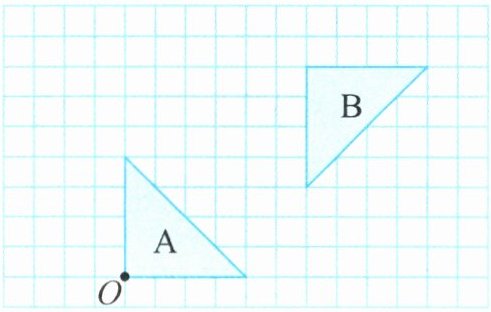
答案： 先将图形A绕点O逆时针旋转$90^{\circ}$，再向右平移10格，最后向上平移3格，就可以拼成一个正方形。(答案不唯一)

5. 说一说涂色部分的图形怎样才能拼在一起，并计算涂色部分的面积。(单位:cm)

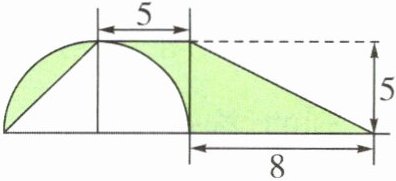
答案： 左边弓形绕半圆的圆心顺时针旋转$90^{\circ}$，即可与右边封闭图形组成一个梯形。
$(5 + 8)\times5\div2 = 32.5(cm^{2})$
解析：左边弓形绕半圆的圆心顺时针旋转$90^{\circ}$后，组合图形的面积可以由两个直角三角形的面积相加求解，也可以直接求梯形的面积。