《2025年高效课堂新疆青少年出版社六年级数学下册北师大版》

1. 判断下列每组中的两个变量是否相关联。是的画“√”，不是的画“×”。
(1)人的身高和跳绳速度。 ( )
(2)圆的半径和直径。 ( )
(3)订《小学生作文》的数量和总价。 ( )
(4)平均每袋米的质量是25千克，米的袋数和总质量。 ( )

答案：
(1)×
(2)√
(3)√
(4)√

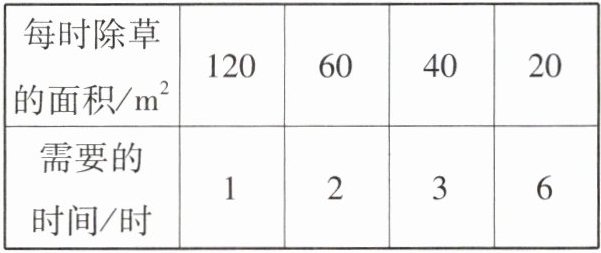
2. 黎叔叔为一片草坪除草，每时除草的面积和需要的时间如下表。
(1)上表中有哪两种量?
(2)表中的两种量是如何变化的?

答案：
(1)每时除草的面积和需要的时间。
(2)需要的时间随着每时除草的面积的变化而变化。每时除草的面积越大，所需要的时间越少。

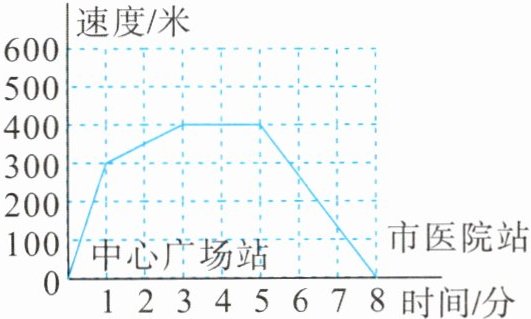
3. (韶关期末真题)下面是1路公共汽车从中心广场站到市医院站之间行驶的时间和速度的关系图。
(1)公共汽车从中心广场站到市医院站之间一共行驶了( )分钟。
(2)在行驶的第1分钟内，汽车的速度从0米/分提高到( )米/分。
(3)在公共汽车从中心广场站到市医院站的过程中，什么时间范围内速度在增大? 什么时间范围内速度保持不变? 什么时间范围内速度在减小?

答案：
(1)8
(2)300
(3)0～3分，速度在增大；3～5分，速度保持不变；5～8分，速度在减小。

4. 小鹏买5个面包和3根香肠共花了14.5元。若一根香肠1.5元，则买4个面包需要多少钱? 如果用x表示购买的面包个数，用y表示购买的香肠根数，用z表示花费的钱数，请用式子表示这三个量之间的关系。

答案： $14.5 - 3×1.5 = 10$（元）
$10÷5 = 2$（元） $4×2 = 8$（元）
$z = 2x + 1.5y$
答：买4个面包需要8元；这三个量之间的关系用式子表示是$z = 2x + 1.5y$。
解析：已知每根香肠1.5元，可求得每个面包2元，由总价 = 单价×数量可得4个面包所花钱数。列式表示购买面包个数$x$、香肠根数$y$与花费钱数$z$的关系为$z = 2x + 1.5y$。