《2025年初中必刷题七年级数学下册浙教版浙江专版》

1[2024浙江杭州调研]如图(1)是生活中常见的晾衣架，其侧面示意图如图(2)所示，则使EG//BH成立的条件是 （ ）

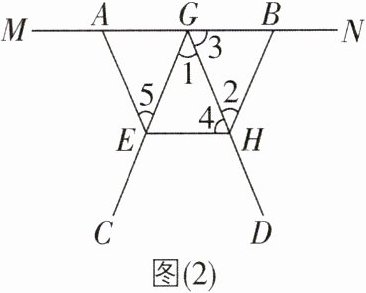
A. ∠1 = ∠5
B. ∠1 = ∠2
C. ∠3 = ∠4
D. ∠4 = ∠5

答案： B

2[2024浙江宁波期末]如图，一条公路的两个拐角∠ABC和∠BCD，若∠ABC = 150°，要使公路AB和CD在同一方向上，则需要使∠BCD = ________°，依据是________________.

答案： 150 内错角相等，两直线平行

3[2024浙江湖州质检]如图，∠1 = ∠2 = 25°，若再添加一个条件使DE//BC，且EF//BD，则添加的条件是________（写出一个即可）.

答案： ∠BDE = 25°（答案不唯一）

4[2024浙江丽水期中]完成下面解题过程.
如图，CB平分∠ACD，∠1 = ∠3. 试说明AB//CD.
解：∵ CB平分∠ACD，
∴ ∠1 = ∠2(________).
∵ ∠1 = ∠3，
∴ ∠2 = ∠_______(________)，
∴ AB//CD(________).

答案： 角平分线的定义@@等量代换@@内错角相等，两直线平行@@3

5[2023浙江温州期末]如图，直线EF分别与直线AB，CD相交于点P和点Q，PG平分∠APQ，QH平分∠DQP，并且∠1 = ∠2，说出图中哪些直线平行，并说明理由.

答案： 【解】AB//CD，PG//QH. 理由：
∵PG平分∠APQ，QH平分∠DQP，
∴∠1 = ∠GPQ = $\frac{1}{2}$∠APQ，∠2 = ∠PQH = $\frac{1}{2}$∠EQD.
∵∠1 = ∠2，
∴∠GPQ = ∠PQH，∠APQ = ∠PQD，
∴PG//QH，AB//CD.

6[2023浙江嘉兴一模]如图，直线a，b被直线c，d所截，下列条件能判定直线a//b的是（ ）


A. ∠1 = ∠2
B. ∠1 = ∠4
C. ∠2 = ∠4
D. ∠3 + ∠4 = 180°

答案： B

7新考向开放性试题如图，在四边形ABCD中，点E是AB延长线上一点，请添加一个条件，使AB//CD，那么可以添加的条件是________（写出一个即可）.

答案： ∠A + ∠D = 180°（答案不唯一）

8[2023浙江绍兴质检]如图所示，∠ABD和∠BDC的平分线交于点E，BE交CD于点F，∠BED = 90°.
(1)AB与CD平行吗？试说明理由.
(2)试探究∠EFD与∠BDE的数量关系，并说明理由.

答案： 【解】（1）AB与CD平行. 理由如下：
∵BE，DE分别平分∠ABD，∠BDC，
∴∠FBD = $\frac{1}{2}$∠ABD，∠BDE = $\frac{1}{2}$∠BDC.
∵∠BED = 90°，
∴∠FBD + ∠BDE = 90°，
∴∠ABD + ∠BDC = 180°，
∴AB//CD.\n（2）∠EFD + ∠BDE = 90°. 理由如下：
∵DE平分∠BDC，
∴∠BDE = ∠FDE.
∵∠BED = 90° = ∠DEF，
∴∠EFD + ∠FDE = 90°，
∴∠EFD + ∠BDE = 90°.