《2025年初中必刷题七年级数学下册浙教版浙江专版》

1[中]一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角度可能是 （ ）
A. 第一次右拐80°，第二次左拐100°
B. 第一次左拐80°，第二次左拐100°
C. 第一次右拐80°，第二次右拐80°
D. 第一次左拐80°，第二次右拐80°

答案： D

2[2024浙江宁波期末，中]如图，若将木条a绕点O旋转后使其与木条b平行，则旋转的最小角度为 （ ）

(第2题图) (第3题图)
A. 65°
B. 85°
C. 95°
D. 115°

答案： B

3[2024浙江温州期末，中]如图，已知∠1 = (3x + 20)°，∠2 = (5x + 20)°，若m//n，则∠1 = ________°。

答案： 72.5

4新考法[中]在同一平面内有2 022条直线a₁，a₂，…，a₂₀₂₂，如果a₁⊥a₂，a₂//a₃，a₃⊥a₄，a₄//a₅，…，那么a₁与a₂₀₂₂的位置关系是________.

答案： 垂直

5[2023辽宁锦州期中，中]学习了平行线后，小敏想出了过已知直线外一点画这条直线的平行线的新方法，她是通过折一张半透明的纸得到的此条直线（如图(1) ~ (4)）. 从图中操作过程你知道小敏画平行线的依据吗？请把你的想法写出来.

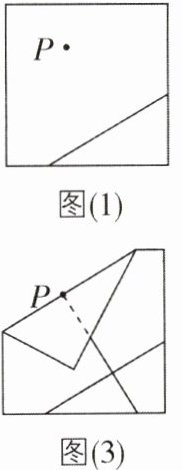
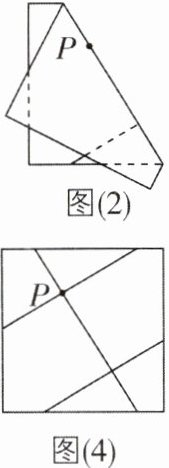
答案：
【解】由图（1）可知，
∵CD⊥PE，AB⊥PE，
∴AB//CD，即在同一平面内，垂直于同一条直线的两条直线互相平行. 或由图（2）可知，
∵AB⊥PE，CD⊥PE，
∴∠1 = ∠2 = 90，
∴AB//CD，即同位角相等，两直线平行.

6[中]在三角形ABC中，∠C = 90°，AM平分∠BAC，D为直线BC上一点，DE⊥AB交直线AB于点E，∠CDE的平分线交直线AC于点F.

(1)如图(1)，当点D在边BC上时，判断DF与AM的位置关系，并说明理由（注：四边形四个角的和为360°）；
(2)①如图(2)，当点D在边BC的延长线上时，DF与AM的位置关系是________；
②如图(3)，当点D在边CB的延长线上时，DF与AM的位置关系是________.

答案：
【解】（1）DF//AM. 理由如下：
∵∠C = 90°，DE⊥AB，
∴∠BAC + ∠CDE = 360° - 90°×2 = 180°.
∵AM平分∠BAC，DF平分∠CDE，
∴∠CAM = $\frac{1}{2}$∠BAC，∠CDF = $\frac{1}{2}$∠CDE，
∴∠CAM + ∠CDF = $\frac{1}{2}$(∠BAC + ∠CDE) = 90°. 又
∵∠CAM + ∠CMA = 180° - ∠C = 90°，
∴∠CDF = ∠CMA，
∴DF//AM.\n（2）①如图（1），延长DF交AM于点N.
∵∠ACB = 90°，DE⊥AB，
∴∠BAC + ∠B = ∠BDE + ∠B = 90°，
∴∠BAC = ∠CDE.
∵AM平分∠BAC，DF平分∠CDE，
∴∠CAM = ∠CDF.
∵∠CAM + ∠AMC = 90°，
∴∠CDF + ∠AMC = 90°，
∴∠DNM = 90°，
∴DF⊥AM. 故答案为DF⊥AM.\n②如图（2），延长AM交DF于点P.
∵∠ACB = 90°，DE⊥AB，
∴∠BAC + ∠ABC = ∠BDE + ∠DBE = 90°.
∵∠ABC = ∠DBE，
∴∠BAC = ∠CDE.
∵AM平分∠BAC，DF平分∠CDE，
∴∠CAM = ∠CDF.
∵∠CDF + ∠F = 90°，
∴∠CAM + ∠F = 90°，
∴∠APF = 90°，
∴DF⊥AM. 故答案为DF⊥AM.

7思想方法分类讨论[难]如图，直线EF上有两点A，C，分别引两条射线AB，CD. ∠BAF = 110°，CD与AB在直线EF两侧. 若∠DCF = 60°，射线AB，CD分别绕A点，C点以1度/秒和6度/秒的速度同时顺时针转动，设转动时间为t秒，在射线CD转动一周的时间内，是否存在某时刻，使得CD与AB平行？若存在，求出所有满足条件的时间t；若不存在，请说明理由.

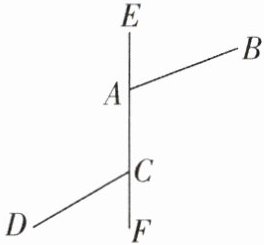
答案：
【解】存在. 分情况讨论：如图（1），当AB与CD在EF的两侧时，(180 - 60)÷6 = 20，
∴0 ＜ t ＜ 20.
∵∠BAF = 110°，∠DCF = 60°，
∴转动t秒时，∠ACD = 180° - 60° - (6t)° = 120° - (6t)°，∠BAC = 110° - t°. 若∠ACD = ∠BAF，即120° - (6t)° = 110° - t°，则AB//CD，解得t = 2. 当t = 20时，CD与CE重合，易知AB//CD不成立.

如图（2），当CD旋转到与AB都在EF的右侧时，(360 - 60)÷6 = 50，
∴20 ＜ t ＜ 50. 此时∠DCF = 360° - (6t)° - 60° = 300° - (6t)°，∠BAC = 110° - t°. 若∠DCF = ∠BAC，即300° - (6t)° = 110° - t°，则AB//CD，解得t = 38. 当t = 50时，CD与CF重合，易知AB//CD不成立. 当CD从EF的右侧再次旋转到EF的左侧，且在旋转一周的时间内时，360÷6 = 60，
∴50 ＜ t≤60，此时AB仍在EF右侧，易知AB//CD的情况不存在. 综上所述，当t的值为2或38时，CD与AB平行.