第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[2024浙江衢州期中,中]若A = (2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)(2³² + 1)×…×(2¹⁰²⁴ + 1) + 1,则A的个位数字为 ( )
A. 2
B. 1
C. 6
D. 8
A. 2
B. 1
C. 6
D. 8
答案:
C 【解析】$A=(2 + 1)(2^{2}+1)(2^{4}+1)(2^{8}+1)(2^{16}+1)(2^{32}+1)\times\cdots\times(2^{1024}+1)+1=(2 - 1)(2 + 1)(2^{2}+1)(2^{4}+1)(2^{8}+1)(2^{16}+1)(2^{32}+1)\times\cdots\times(2^{1024}+1)+1=2^{2048}-1 + 1 = 2^{2048}$. $\because 2^{1}=2$,$2^{2}=4$,$2^{3}=8$,$2^{4}=16$,$2^{5}=32$,$2^{6}=64$,$2^{7}=128$,$2^{8}=256$,$2^{9}=512$,$\cdots$,$\therefore 2^{1}$,$2^{2}$,$2^{3}$,$\cdots$的个位数字按$2$,$4$,$8$,$6$依次循环. $\because 2048\div4 = 512$,$\therefore 2^{2048}$的个位数字与$2^{4}$的个位数字相同,$\therefore 2^{2048}$的个位数字为$6$. 故选C.
2[中]已知x - $\frac{1}{x}$ = 4,则x² + $\frac{1}{x²}$的值为 ( )
A. 6
B. 16
C. 14
D. 18
A. 6
B. 16
C. 14
D. 18
答案:
D 【解析】$\because x-\frac{1}{x}=4$,$\therefore(x-\frac{1}{x})^{2}=x^{2}-2\times x\times\frac{1}{x}+\frac{1}{x^{2}}=16$,$\therefore x^{2}+\frac{1}{x^{2}}=18$,故选D.
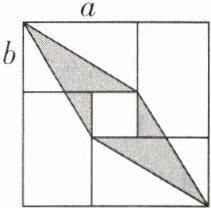
3[2024浙江杭州调研,中]若将四张长为a、宽为b(a > b)的长方形纸片按如图所示的方式拼成一个边长为a + b的正方形,则图中阴影部分的面积为 ( )
A. 2ab - b²
B. 2ab - 2b²
C. a² - 4b²
D. 2b² - ab

A. 2ab - b²
B. 2ab - 2b²
C. a² - 4b²
D. 2b² - ab
答案:
B 【解析】阴影部分的面积为$(a + b)^{2}-\frac{(b + a + b)\times b}{2}-\frac{1}{2}ab-\frac{1}{2}ab-\frac{(b + a + b)\times b}{2}-(a - b)^{2}=(a + b)^{2}-(a + 2b)\times b - ab-(a - b)^{2}=a^{2}+2ab + b^{2}-ab-2b^{2}-ab-a^{2}+2ab - b^{2}=2ab-2b^{2}$. 故选B.
4[2024浙江台州质检,较难]已知(x - 2023)² + (x - 2025)² = 4050,则(x - 2024)²的值是 ( )
A. 1
B. 2025
C. 2024
D. 2023
A. 1
B. 2025
C. 2024
D. 2023
答案:
C 【解析】$\because(x - 2023)-(x - 2025)=2$,$\therefore(x - 2023)^{2}-2(x - 2023)(x - 2025)+(x - 2025)^{2}=4$. $\because(x - 2023)^{2}+(x - 2025)^{2}=4050$,$\therefore 2(x - 2023)(x - 2025)=4046$,$\therefore(x - 2023)(x - 2025)=2023$,$\therefore(x - 2024 + 1)(x - 2024 - 1)=2023$,$\therefore(x - 2024)^{2}-1 = 2023$,$\therefore(x - 2024)^{2}=2024$. 故选C.
5[2023浙江丽水中,中]若关于x的多项式4x² + (m - 1)x + 9是完全平方式,则m的值为________.
答案:
13或 - 11 【解析】$\because$关于$x$的多项式$4x^{2}+(m - 1)x + 9$是完全平方式,$\therefore(m - 1)x=\pm2\times3\times2x$. 当$(m - 1)x = 2\times3\times2x = 12x$时,$m = 13$;当$(m - 1)x=-2\times3\times2x=-12x$时,$m=-11$. 综上所述,$m$的值为$13$或$-11$.
6[中]若A = x² + 2x - 6y,B = -y² + 4x - 11,则A,B的大小关系为________.
答案:
$A>B$ 【解析】$A - B=x^{2}+2x-6y-(-y^{2}+4x - 11)=x^{2}+2x-6y + y^{2}-4x + 11=x^{2}-2x + y^{2}-6y + 11=x^{2}-2x + 1 + y^{2}-6y + 9=(x - 1)^{2}+(y - 3)^{2}+1$. $\because(x - 1)^{2}\geqslant0$,$(y - 3)^{2}\geqslant0$,$\therefore(x - 1)^{2}+(y - 3)^{2}+1>0$,即$A - B>0$,$\therefore A>B$. 故答案为$A>B$.
7[2023湖北黄冈质检,中]已知实数x,y,z满足x² + y² + z² = 4,则(2x - y)² + (2y - z)² + (2z - x)²的最大值是________.
答案:
28 【解析】$\because$实数$x$,$y$,$z$满足$x^{2}+y^{2}+z^{2}=4$,$\therefore(2x - y)^{2}+(2y - z)^{2}+(2z - x)^{2}=5(x^{2}+y^{2}+z^{2})-4(xy + yz + xz)=20-2[(x + y + z)^{2}-(x^{2}+y^{2}+z^{2})]=28-2(x + y + z)^{2}\leqslant28$,$\therefore$当$x + y + z = 0$时,$(2x - y)^{2}+(2y - z)^{2}+(2z - x)^{2}$有最大值,最大值是$28$. 故答案为$28$.
8[中]有一系列等式:
1×2×3×4 + 1 = 5² = (1² + 3×1 + 1)²;
2×3×4×5 + 1 = 11² = (2² + 3×2 + 1)²;
3×4×5×6 + 1 = 19² = (3² + 3×3 + 1)²;
4×5×6×7 + 1 = 29² = (4² + 3×4 + 1)²;
……
(1)根据你的观察、归纳及发现的规律,写出8×9×10×11 + 1的结果为________.
(2)试猜想n(n + 1)(n + 2)(n + 3) + 1是哪一个数的平方,并说明理由.
1×2×3×4 + 1 = 5² = (1² + 3×1 + 1)²;
2×3×4×5 + 1 = 11² = (2² + 3×2 + 1)²;
3×4×5×6 + 1 = 19² = (3² + 3×3 + 1)²;
4×5×6×7 + 1 = 29² = (4² + 3×4 + 1)²;
……
(1)根据你的观察、归纳及发现的规律,写出8×9×10×11 + 1的结果为________.
(2)试猜想n(n + 1)(n + 2)(n + 3) + 1是哪一个数的平方,并说明理由.
答案:
【解】
(1)根据题意,得$8\times9\times10\times11 + 1=(8^{2}+3\times8 + 1)^{2}=89^{2}$. 故答案为$89^{2}$.
(2)猜想:$n(n + 1)(n + 2)(n + 3)+1=(n^{2}+3n + 1)^{2}$. 理由如下:等式左边$=(n^{2}+3n)(n^{2}+3n + 2)+1=n^{4}+3n^{3}+2n^{2}+3n^{3}+9n^{2}+6n + 1=n^{4}+6n^{3}+11n^{2}+6n + 1$,等式右边$=(n^{2}+3n + 1)^{2}=(n^{2}+1)^{2}+2\cdot3n\cdot(n^{2}+1)+9n^{2}=n^{4}+2n^{2}+1+6n^{3}+6n + 9n^{2}=n^{4}+6n^{3}+11n^{2}+6n + 1$,所以左边$=$右边.
(1)根据题意,得$8\times9\times10\times11 + 1=(8^{2}+3\times8 + 1)^{2}=89^{2}$. 故答案为$89^{2}$.
(2)猜想:$n(n + 1)(n + 2)(n + 3)+1=(n^{2}+3n + 1)^{2}$. 理由如下:等式左边$=(n^{2}+3n)(n^{2}+3n + 2)+1=n^{4}+3n^{3}+2n^{2}+3n^{3}+9n^{2}+6n + 1=n^{4}+6n^{3}+11n^{2}+6n + 1$,等式右边$=(n^{2}+3n + 1)^{2}=(n^{2}+1)^{2}+2\cdot3n\cdot(n^{2}+1)+9n^{2}=n^{4}+2n^{2}+1+6n^{3}+6n + 9n^{2}=n^{4}+6n^{3}+11n^{2}+6n + 1$,所以左边$=$右边.
9核心素养·几何直观[2023江苏镇江期末,较难]
(1)从图(1)~(3)中任意选择一个,通过计算图中阴影部分的面积,可得到关于a,b的等量关系是________.
(2)尝试解决:①已知:m + n = 2,m² + n² = 7,则mn = ________;
②已知:2a + b = 3,ab = 1,求(2a - b)²的值;
③已知:(4 - x)(5 - x) = 6,求(4 - x)² + (5 - x)²的值.
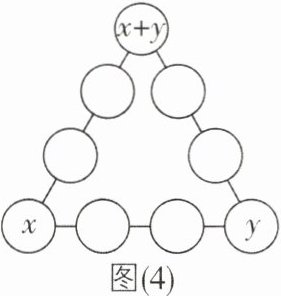
(3)填数游戏:如图(4),把数字1~9填入构成三角形形状的9个圆圈中,使得各边上的四个数字的和都等于21,将每边四个数字的平方和分别记作A,B,C,已知A + B + C = 411. 如果将位于这个三角形顶点处的三个圆圈填入的数字分别表示为x,y,x + y,求xy的值.
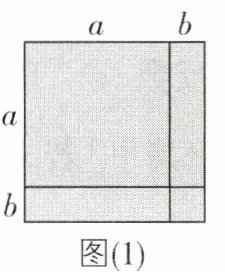
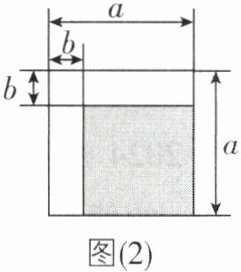

(1)从图(1)~(3)中任意选择一个,通过计算图中阴影部分的面积,可得到关于a,b的等量关系是________.
(2)尝试解决:①已知:m + n = 2,m² + n² = 7,则mn = ________;
②已知:2a + b = 3,ab = 1,求(2a - b)²的值;
③已知:(4 - x)(5 - x) = 6,求(4 - x)² + (5 - x)²的值.
(3)填数游戏:如图(4),把数字1~9填入构成三角形形状的9个圆圈中,使得各边上的四个数字的和都等于21,将每边四个数字的平方和分别记作A,B,C,已知A + B + C = 411. 如果将位于这个三角形顶点处的三个圆圈填入的数字分别表示为x,y,x + y,求xy的值.




答案:
【解】
(1)题图
(1):$(a + b)^{2}=a^{2}+2ab + b^{2}$; 题图
(2):$(a - b)^{2}=a^{2}-2ab + b^{2}$; 题图
(3):$4ab=(a + b)^{2}-(a - b)^{2}$. 故答案为$(a + b)^{2}=a^{2}+2ab + b^{2}$(或$(a - b)^{2}=a^{2}-2ab + b^{2}$或$4ab=(a + b)^{2}-(a - b)^{2}$).
(2)①$\because m + n = 2$,$\therefore(m + n)^{2}=m^{2}+2mn + n^{2}=4$. $\because m^{2}+n^{2}=7$,$\therefore 7+2mn = 4$,$\therefore mn=-\frac{3}{2}$,故答案为$-\frac{3}{2}$. ②$\because(2a - b)^{2}=(2a + b)^{2}-8ab$,$2a + b = 3$,$ab = 1$,$\therefore(2a - b)^{2}=3^{2}-8\times1 = 1$. ③$\because(4 - x)^{2}+(5 - x)^{2}=[(4 - x)-(5 - x)]^{2}+2(4 - x)(5 - x)=1+2(4 - x)(5 - x)=1+2\times6 = 13$.
(3)数字$1~9$的和为$1 + 2+3 + 4+5 + 6+7 + 8+9 = 45$. $\because$各边上的四个数字的和都等于$21$,$\therefore 21\times3-45 = 18$,$\therefore x + y+(x + y)=18$,即$x + y = 9$. $\because$每边四个数字的平方和分别记作$A$,$B$,$C$,且$A + B + C = 411$,又$1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+6^{2}+7^{2}+8^{2}+9^{2}=285$,$\therefore x^{2}+y^{2}+(x + y)^{2}=411-285 = 126$,$\therefore x^{2}+y^{2}+81 = 126$,$\therefore x^{2}+y^{2}=45$,$\therefore(x + y)^{2}-2xy = 45$,$\therefore xy = 18$.
(1)题图
(1):$(a + b)^{2}=a^{2}+2ab + b^{2}$; 题图
(2):$(a - b)^{2}=a^{2}-2ab + b^{2}$; 题图
(3):$4ab=(a + b)^{2}-(a - b)^{2}$. 故答案为$(a + b)^{2}=a^{2}+2ab + b^{2}$(或$(a - b)^{2}=a^{2}-2ab + b^{2}$或$4ab=(a + b)^{2}-(a - b)^{2}$).
(2)①$\because m + n = 2$,$\therefore(m + n)^{2}=m^{2}+2mn + n^{2}=4$. $\because m^{2}+n^{2}=7$,$\therefore 7+2mn = 4$,$\therefore mn=-\frac{3}{2}$,故答案为$-\frac{3}{2}$. ②$\because(2a - b)^{2}=(2a + b)^{2}-8ab$,$2a + b = 3$,$ab = 1$,$\therefore(2a - b)^{2}=3^{2}-8\times1 = 1$. ③$\because(4 - x)^{2}+(5 - x)^{2}=[(4 - x)-(5 - x)]^{2}+2(4 - x)(5 - x)=1+2(4 - x)(5 - x)=1+2\times6 = 13$.
(3)数字$1~9$的和为$1 + 2+3 + 4+5 + 6+7 + 8+9 = 45$. $\because$各边上的四个数字的和都等于$21$,$\therefore 21\times3-45 = 18$,$\therefore x + y+(x + y)=18$,即$x + y = 9$. $\because$每边四个数字的平方和分别记作$A$,$B$,$C$,且$A + B + C = 411$,又$1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+6^{2}+7^{2}+8^{2}+9^{2}=285$,$\therefore x^{2}+y^{2}+(x + y)^{2}=411-285 = 126$,$\therefore x^{2}+y^{2}+81 = 126$,$\therefore x^{2}+y^{2}=45$,$\therefore(x + y)^{2}-2xy = 45$,$\therefore xy = 18$.
查看更多完整答案,请扫码查看


