第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[中]如图,AD//BE,AC与BC相交于点C,且∠1 = $\frac{1}{n}$∠DAB,∠2 = $\frac{1}{n}$∠EBA。若∠C = 45°,则n = ( )
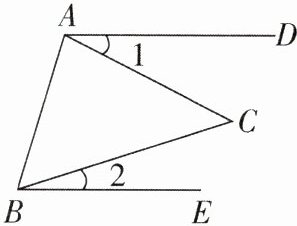
A. 2
B. 3
C. 4
D. 5

A. 2
B. 3
C. 4
D. 5
答案:
C
2[2024浙江湖州调研,中]如图(1)为某校放置在水平操场上的篮球架,图(2)为其侧面示意图,初始状态时,篮球架的横梁EF平行于AB,主柱AD垂直于地面,EF与上拉杆CF形成的角为∠F,且∠F = 150°,这一篮球架可以通过调整CF和后拉杆BC的位置来调整EF的高度.在调整EF的高度时,为使EF和AB平行,需要改变∠F和∠C的度数,调整EF使其上升到GH的位置,此时GH与AB平行,∠CDB = 35°,并且点H,D,B在同一直线上,则∠H为________°。
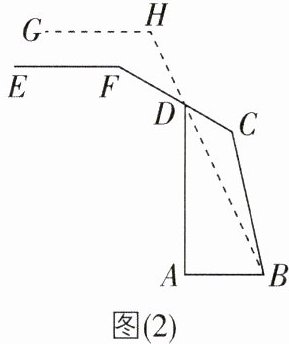


答案:
115
3[2023重庆沙坪坝区期中,较难]如图(1),将一条对边平行的围巾折叠,并将其抽象成相应的数学模型如图(2),AB//CD,折痕分别为AD,CB。若∠DAB = 2∠GCB,DF//CG,则∠ADF等于________。



答案:
60°
4[2023吉林长春期末,中]
(1)如图(1),若AB//CD,∠BEP = 25°,∠PFD = 30°,则∠EPF = ________°。
(2)如图(1),若AB//CD,请猜想∠BEP,∠PFD,∠EPF之间有何数量关系?请说明理由。
(3)如图(2),AB//CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?
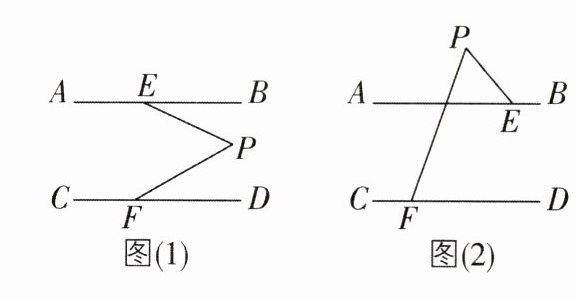
(1)如图(1),若AB//CD,∠BEP = 25°,∠PFD = 30°,则∠EPF = ________°。
(2)如图(1),若AB//CD,请猜想∠BEP,∠PFD,∠EPF之间有何数量关系?请说明理由。
(3)如图(2),AB//CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?

答案:
55@@∠EPF = ∠BEP + ∠PFD。理由如下:如图(1),因为AB//CD,所以AB//PM//CD,所以∠1 = ∠BEP,∠2 = ∠PFD,所以∠EPF = ∠1 + ∠2 = ∠BEP + ∠PFD。@@∠PFC = ∠PEA + ∠EPF。理由如下:如图(2),过P点作PN//AB。因为AB//CD,所以AB//PN//CD,所以∠PEA = ∠NPE,∠FPN = ∠PFC,所以∠PFC = ∠FPN = ∠NPE + ∠EPF = ∠PEA + ∠EPF。

55@@∠EPF = ∠BEP + ∠PFD。理由如下:如图(1),因为AB//CD,所以AB//PM//CD,所以∠1 = ∠BEP,∠2 = ∠PFD,所以∠EPF = ∠1 + ∠2 = ∠BEP + ∠PFD。@@∠PFC = ∠PEA + ∠EPF。理由如下:如图(2),过P点作PN//AB。因为AB//CD,所以AB//PN//CD,所以∠PEA = ∠NPE,∠FPN = ∠PFC,所以∠PFC = ∠FPN = ∠NPE + ∠EPF = ∠PEA + ∠EPF。

5[2023江苏南通启东期末,较难]已知点D在∠ABC内,E为射线BC上一点,连结DE,CD.
(1)如图(1)所示,连结AE,若∠AED = ∠BAE + ∠CDE.
①线段AB与CD有何位置关系?请说明理由.
②过点D作DM//AE交射线BC于点M,试说明:∠CDM = ∠BAE。
(2)如图(2)所示,∠AED = ∠A - ∠D,若M为平面内一动点,MA//ED,请直接写出∠MAB与∠CDE的数量关系。
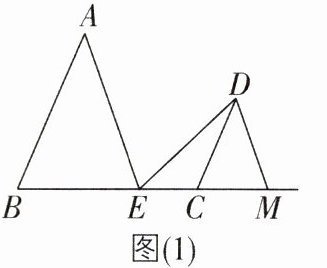
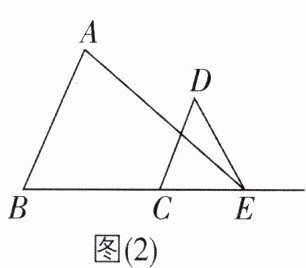
(1)如图(1)所示,连结AE,若∠AED = ∠BAE + ∠CDE.
①线段AB与CD有何位置关系?请说明理由.
②过点D作DM//AE交射线BC于点M,试说明:∠CDM = ∠BAE。
(2)如图(2)所示,∠AED = ∠A - ∠D,若M为平面内一动点,MA//ED,请直接写出∠MAB与∠CDE的数量关系。


答案:
AB//CD。理由:过点E作EF//AB,如图(1),则∠AEF = ∠BAE。因为∠AED = ∠BAE + ∠CDE,∠AED = ∠AEF + ∠FED,所以∠CDE = ∠FED,所以FE//CD。因为AB//EF,所以AB//CD。@@因为DM//AE,所以∠AED = ∠MDE。因为∠CDE = ∠FED,所以∠MDC = ∠AEF。因为∠AEF = ∠BAE,所以∠CDM = ∠BAE。@@∠MAB = ∠CDE或∠MAB + ∠CDE = 180°。 ①当点M在AB的右侧时,如图(2),∠MAB = ∠CDE。理由:设AE与CD交于点F。因为∠CFE = ∠D + ∠AED,所以∠AED = ∠CFE - ∠D。因为∠AED = ∠BAE - ∠D,所以∠BAE = ∠CFE,所以AB//CD,所以∠ABC = ∠DCE。因为AM//DE,所以∠AMB = ∠DEC。因为∠MAB = 180° - ∠ABC - ∠AMB,∠CDE = 180° - ∠DCE - ∠DEC,所以∠MAB = ∠CDE。 ②当点M在AB的左侧时,如图(3),∠MAB + ∠CDE = 180°。理由:由(2)①可知∠BAN = ∠CDE。因为∠BAN + ∠BAM = 180°,所以∠MAB + ∠CDE = 180°。综上,∠MAB与∠CDE的数量关系为∠MAB = ∠CDE或∠MAB + ∠CDE = 180°。

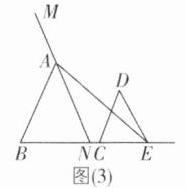
AB//CD。理由:过点E作EF//AB,如图(1),则∠AEF = ∠BAE。因为∠AED = ∠BAE + ∠CDE,∠AED = ∠AEF + ∠FED,所以∠CDE = ∠FED,所以FE//CD。因为AB//EF,所以AB//CD。@@因为DM//AE,所以∠AED = ∠MDE。因为∠CDE = ∠FED,所以∠MDC = ∠AEF。因为∠AEF = ∠BAE,所以∠CDM = ∠BAE。@@∠MAB = ∠CDE或∠MAB + ∠CDE = 180°。 ①当点M在AB的右侧时,如图(2),∠MAB = ∠CDE。理由:设AE与CD交于点F。因为∠CFE = ∠D + ∠AED,所以∠AED = ∠CFE - ∠D。因为∠AED = ∠BAE - ∠D,所以∠BAE = ∠CFE,所以AB//CD,所以∠ABC = ∠DCE。因为AM//DE,所以∠AMB = ∠DEC。因为∠MAB = 180° - ∠ABC - ∠AMB,∠CDE = 180° - ∠DCE - ∠DEC,所以∠MAB = ∠CDE。 ②当点M在AB的左侧时,如图(3),∠MAB + ∠CDE = 180°。理由:由(2)①可知∠BAN = ∠CDE。因为∠BAN + ∠BAM = 180°,所以∠MAB + ∠CDE = 180°。综上,∠MAB与∠CDE的数量关系为∠MAB = ∠CDE或∠MAB + ∠CDE = 180°。


查看更多完整答案,请扫码查看


