《2025年初中必刷题七年级数学下册浙教版浙江专版》

1[2024浙江杭州期中]下列多项式的乘法中，能用平方差公式计算的是 （ ）
A. (2a - 3b)(3b + 2a)
B. (2a + b)(2b - a)
C. (3m - n)(-3m + n)
D. ($\frac{2}{3}m - n$)(-n + $\frac{2}{3}m$)

答案： A 【解析】A选项，$(2a - 3b)(3b + 2a)=4a^{2}-9b^{2}$，能用平方差公式计算，符合题意；B选项，$(2a + b)(2b - a)$不能用平方差公式计算，不符合题意；C选项，$(3m - n)(-3m + n)=-(3m - n)(3m - n)$，不能用平方差公式计算，不符合题意；D选项，$(\frac{2}{3}m - n)(-n+\frac{2}{3}m)$不能用平方差公式计算，不符合题意. 故选A.

2下列多项式的乘法中，不能用平方差公式计算的是 （ ）
A. (4x - 3y)(-3y - 4x)
B. (a + b - c)(-c + b + a)
C. (-x + y)(x - y)
D. (2x² - y²)(2x² + y²)

答案： C 【解析】A选项，原式$=(-3y)^{2}-(4x)^{2}$，该选项不符合题意；B选项，原式$=(a - c)^{2}-b^{2}$，该选项不符合题意；C选项，没有完全相同的项，不能用平方差公式计算，该选项符合题意；D选项，原式$=(2x^{2})^{2}-(y^{2})^{2}$，该选项不符合题意. 故选C.

3[2023湖南娄底中考]下列运算正确的是 （ ）
A. a²·a⁴ = a⁸
B. a² + 3a = 4a²
C. (a + 2)(a - 2) = a² - 2
D. (-2a²b)³ = -8a⁶b³

答案： D 【解析】$a^{2}\cdot a^{4}=a^{6}$，故A不符合题意；$a^{2}$与$3a$不是同类项，不能合并，故B不符合题意；$(a + 2)(a - 2)=a^{2}-4$，故C不符合题意；$(-2a^{2}b)^{3}=-8a^{6}b^{3}$，故D符合题意. 故选D.

4[2024湖北咸宁质检]已知(x + 2)(x - 2) - 2x = 1，则2x² - 4x + 5的值是 （ ）
A. -3
B. 8
C. 13
D. 15

答案： D 【解析】$\because(x + 2)(x - 2)-2x = 1$，$\therefore x^{2}-4-2x = 1$，$\therefore x^{2}-2x = 5$，$\therefore 2x^{2}-4x + 5 = 2(x^{2}-2x)+5 = 2×5 + 5 = 10 + 5 = 15$. 故选D.

5[2024浙江宁波期末]计算(x + 2)(x² + 4)(x - 2) - x⁴ + 16的结果是 （ ）
A. 2x³
B. -32
C. 0
D. 78

答案： C 【解析】$(x + 2)(x^{2}+4)(x - 2)-x^{4}+16=[(x + 2)(x - 2)](x^{2}+4)-x^{4}+16=(x^{2}-4)(x^{2}+4)-x^{4}+16=x^{4}-16-x^{4}+16 = 0$，故选C.

6[2023福建厦门期中]若a = 1，b = 2023×2021 - 2022²，c = (-$\frac{2}{3}$)²⁰²²×($\frac{3}{2}$)²⁰²³，则下列a，b，c的大小关系正确的是 （ ）
A. b ＜ a ＜ c
B. a ＜ b ＜ c
C. a ＜ c ＜ b
D. c ＜ b ＜ a

答案： A 【解析】$\because a = 1$，$b = 2023×2021-2022^{2}=(2022 + 1)(2022 - 1)-2022^{2}=2022^{2}-1-2022^{2}=-1$，$c = (-\frac{2}{3})^{2022}×(\frac{3}{2})^{2023}=(-\frac{2}{3}×\frac{3}{2})^{2022}×\frac{3}{2}=(-1)^{2022}×\frac{3}{2}=\frac{3}{2}$，$\therefore b\lt a\lt c$，故选A.

7[2023浙江湖州期中]若(a² + b² + 1)(a² + b² - 1) = 35，则a² + b² = ________.

答案： 6 【解析】$\because(a^{2}+b^{2}+1)(a^{2}+b^{2}-1)=35$，$\therefore[(a^{2}+b^{2})+1][(a^{2}+b^{2})-1]=35$，$\therefore(a^{2}+b^{2})^{2}-1 = 35$，$\therefore(a^{2}+b^{2})^{2}=36$. $\because a^{2}+b^{2}\geqslant0$，$\therefore a^{2}+b^{2}=6$. 故答案为6.

8[2023浙江温州龙湾区期中]若x² - y² = 44，x - y = 11，则x + y = ________.

答案： 4 【解析】因为$x^{2}-y^{2}=(x + y)(x - y)$，所以$x + y=(x^{2}-y^{2})\div(x - y)=44\div11 = 4$. 故答案为4.

9阅读材料后解决问题：
小明遇到下面一个问题：计算(2 + 1)(2² + 1)·(2⁴ + 1)(2⁸ + 1).
经过观察，小明发现将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：
(2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1) = (2 - 1)(2 + 1)·(2² + 1)(2⁴ + 1)(2⁸ + 1) = (2² - 1)·(2² + 1)(2⁴ + 1)(2⁸ + 1) = (2⁴ - 1)(2⁴ + 1)(2⁸ + 1) = (2⁸ - 1)·(2⁸ + 1) = 2¹⁶ - 1.
请你仿照小明解决问题的方法，尝试计算：(6 + 1)(6² + 1)(6⁴ + 1)(6⁸ + 1) = ________.

答案： $\frac{6^{16}-1}{5}$ 【解析】根据题意得，原式$=\frac{1}{5}×(6 - 1)(6 + 1)(6^{2}+1)(6^{4}+1)(6^{8}+1)=\frac{1}{5}×(6^{2}-1)(6^{2}+1)(6^{4}+1)(6^{8}+1)=\frac{1}{5}×(6^{4}-1)(6^{4}+1)(6^{8}+1)=\frac{1}{5}×(6^{8}-1)(6^{8}+1)=\frac{1}{5}×(6^{16}-1)=\frac{6^{16}-1}{5}$. 故答案为$\frac{6^{16}-1}{5}$.

10[2023浙江嘉兴期末]计算：
(1)(3 + 4y)(4y - 3) - (x - 4y)².
(2)(2a - 3b)² - (b + 3a)(3a - b).

答案： 【解】
(1)原式$=(4y + 3)(4y - 3)-(x - 4y)(x - 4y)=16y^{2}-9-(x^{2}-8xy + 16y^{2})=16y^{2}-9-x^{2}+8xy-16y^{2}=-9-x^{2}+8xy$.
(2)原式$=(2a - 3b)(2a - 3b)-(3a + b)(3a - b)=4a^{2}-12ab + 9b^{2}-(9a^{2}-b^{2})=4a^{2}-12ab + 9b^{2}+b^{2}-9a^{2}=10b^{2}-5a^{2}-12ab$.

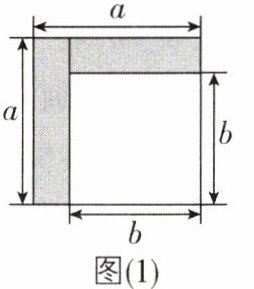
11[2024浙江金华调研]从边长为a的正方形纸片中剪去一个边长为b的正方形(如图(1))，然后将剩余部分剪拼成一个长方形(如图(2))，上述操作能验证的等式是________.

答案： $(a + b)(a - b)=a^{2}-b^{2}$ 【解析】题图
(1)中阴影部分可以看作两个正方形的面积差，即$a^{2}-b^{2}$，题图
(2)是长为$a + b$、宽为$a - b$的长方形，因此其面积为$(a + b)(a - b)$，所以有$(a + b)(a - b)=a^{2}-b^{2}$. 故答案为$(a + b)(a - b)=a^{2}-b^{2}$.

12[2024浙江湖州期中]如图，若大正方形与小正方形的面积之差为20，则阴影部分的面积是________.

答案： 10 【解析】设大正方形的边长为$a$，小正方形的边长为$b$，由题意和题图可知$a^{2}-b^{2}=20$，$AE=a - b$，$BC = a$，$BD = b$，$\therefore S_{阴影}=S_{\triangle ACE}+S_{\triangle ADE}=\frac{1}{2}AE\cdot BC+\frac{1}{2}AE\cdot BD=\frac{1}{2}AE\cdot(BC + BD)=\frac{1}{2}(a - b)\cdot(a + b)=\frac{1}{2}(a^{2}-b^{2})=\frac{1}{2}×20 = 10$. 故答案为10.