《2025年初中必刷题七年级数学下册浙教版浙江专版》

1[2024 浙江杭州质检]a,b,c 为同一平面内的任意三条直线,它们的交点个数可能为 （ ）
A. 1 或 2 或 3
B. 0 或 1 或 2 或 3
C. 1 或 2
D. 以上都不对

答案： B

2[2024 浙江衢州期末]下列各图中,∠1 与∠2是对顶角的是 （ ）

答案： C

3 如图,直线 a,b,c 相交于一点,则∠1+∠2+∠3的度数为 （ ）

A. 90°
B. 120°
C. 135°
D. 180°

答案： D

4[2024 浙江宁波期中]如图,直线 AB,CD 相交于点 O,OE 平分∠BOD,若∠AOC = 40°,则∠COE 的度数为 （ ）

A. 145°
B. 150°
C. 155°
D. 160°

答案： D

5[2024 浙江温州调研]三条直线相交于一点,共形成________对顶角.

答案： 6

6[2024 浙江杭州期末]平面内有五条直线两两相交,设最多有 a 个交点,最少有 b 个交点,最多有 c 对对顶角,则2a+b - c 的值是________.

答案： 1

7 如图,直线 a,b 相交于点 O,将半圆形量角器的圆心与点 O 重合,发现表示 60°的刻度线与直线 a 重合,表示 138°的刻度线与直线 b 重合,则∠1 =________°.

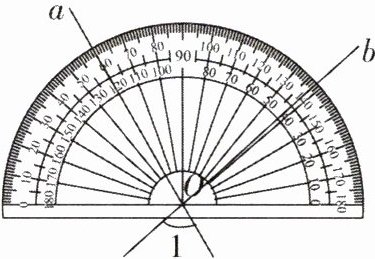
答案： 78

8[2024 浙江杭州期末]如图,已知直线 AB 与直线 CD 相交于点 O,∠BOD = α,OE 为平面内一条射线,∠BOE 与∠AOC 互补,ON 是∠AOC 的平分线.
（1）∠BOD 和∠AOE 相等吗? 请说明理由.
（2）射线 OM 平分∠AOD,求∠MON 的度数.
（3）在（2）的条件下,若∠EOM = $\frac{1}{3}$∠MON,求α的度数.

答案： 【解】 （1）相等. 理由：由题意可知，∠BOE + ∠AOC = 180°，∠BOE + ∠AOE = 180°，
∴∠AOE = ∠AOC.
∵∠BOD = ∠AOC，
∴∠BOD = ∠AOE. （2）如图所示.
∵∠BOD = ∠AOC = α，
∴∠AOD = 180° - α.
∵ON，OM分别是∠AOC，∠AOD的平分线，
∴∠AON = $\frac{1}{2}$∠AOC = $\frac{1}{2}$α，∠AOM = $\frac{1}{2}$∠AOD = 90° - $\frac{1}{2}$α，
∴∠MON = ∠AON + ∠AOM = $\frac{1}{2}$α + 90° - $\frac{1}{2}$α = 90°. （3）
∵∠EOM = $\frac{1}{3}$∠MON = $\frac{1}{3}\times90° = 30°$，∠AOE = α，∠AON = $\frac{1}{2}$α，
∴∠MON = ∠MOE + ∠AOE + ∠AON = 30° + α + $\frac{1}{2}$α = 90°，解得α = 40°.

9 已知直线 AB 和 CD 相交于点 O,射线 OE 将∠AOC 分成两部分,射线 OF 为∠BOE 的平分线. 若|∠BOF - ∠AOE| = 36°,则锐角∠BOF =________.

答案： 48°或72°