第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
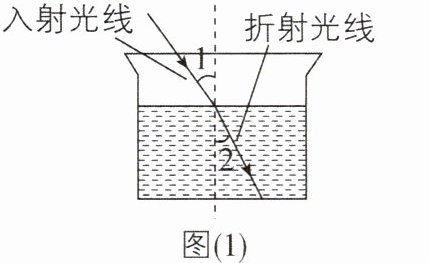
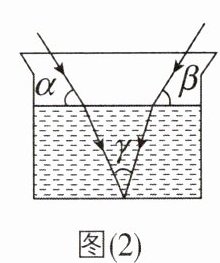
1新考向|跨学科综合[中]如图(1),当光线从空气进入水中时,会发生折射,满足入射角∠1与折射角∠2的度数比为4∶3. 如图(2),在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面夹角分别为α,β,在水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )
A. $\frac{3}{4}(\alpha+\beta)=\gamma$
B. $\frac{3}{4}(\alpha+\beta)=135^{\circ}-\gamma$
C. $\alpha+\beta=\gamma$
D. $\alpha+\beta+\gamma = 180^{\circ}$


A. $\frac{3}{4}(\alpha+\beta)=\gamma$
B. $\frac{3}{4}(\alpha+\beta)=135^{\circ}-\gamma$
C. $\alpha+\beta=\gamma$
D. $\alpha+\beta+\gamma = 180^{\circ}$
答案:
B【解析】如图,过点$B$,$D$,$F$分别作水面的垂线,则$PC// DE// QG$,所以$\angle BDE=\angle DBC$,$\angle FDE=\angle DFG$,所以$\angle BDF=\angle BDE+\angle FDE=\angle DBC+\angle DFG$。由题可得,$\angle DBC=\frac{3}{4}\angle ABP=\frac{3}{4}(90^{\circ}-\alpha)$,$\angle DFG=\frac{3}{4}\angle HFQ=\frac{3}{4}(90^{\circ}-\beta)$,所以$\angle BDF=\frac{3}{4}(90^{\circ}-\alpha)+\frac{3}{4}(90^{\circ}-\beta)=\frac{3}{4}(180^{\circ}-\alpha-\beta)$,即$\gamma = 135^{\circ}-\frac{3}{4}(\alpha+\beta)$,所以$\frac{3}{4}(\alpha+\beta)=135^{\circ}-\gamma$,故选B。
B【解析】如图,过点$B$,$D$,$F$分别作水面的垂线,则$PC// DE// QG$,所以$\angle BDE=\angle DBC$,$\angle FDE=\angle DFG$,所以$\angle BDF=\angle BDE+\angle FDE=\angle DBC+\angle DFG$。由题可得,$\angle DBC=\frac{3}{4}\angle ABP=\frac{3}{4}(90^{\circ}-\alpha)$,$\angle DFG=\frac{3}{4}\angle HFQ=\frac{3}{4}(90^{\circ}-\beta)$,所以$\angle BDF=\frac{3}{4}(90^{\circ}-\alpha)+\frac{3}{4}(90^{\circ}-\beta)=\frac{3}{4}(180^{\circ}-\alpha-\beta)$,即$\gamma = 135^{\circ}-\frac{3}{4}(\alpha+\beta)$,所以$\frac{3}{4}(\alpha+\beta)=135^{\circ}-\gamma$,故选B。

2[2024浙江诸暨期末,较难]如图,直线AB//CD,现将两个直角三角尺按如下步骤及要求摆放于同一平面内:
步骤1:将一个含30°角(∠GFE = 30°)的直角三角尺(三角形EFG)如图放置,使得点E,F落在直线CD上,直角顶点G位于两平行线之间;
步骤2:将另一个含45°角(∠MPN = ∠MNP = 45°)的直角三角尺(三角形PMN)进行放置,使得点P落于直线AB上(点P在点A的右边),边MN经过点G,满足∠EGN = 40°.
根据以上步骤及要求,∠APM的度数可以是①~⑥中的( )
①10°;②20°;③70°;④80°;⑤160°;⑥170°.

A. ①③⑥
B. ①④⑥
C. ②④⑤
D. ②③⑤
步骤1:将一个含30°角(∠GFE = 30°)的直角三角尺(三角形EFG)如图放置,使得点E,F落在直线CD上,直角顶点G位于两平行线之间;
步骤2:将另一个含45°角(∠MPN = ∠MNP = 45°)的直角三角尺(三角形PMN)进行放置,使得点P落于直线AB上(点P在点A的右边),边MN经过点G,满足∠EGN = 40°.
根据以上步骤及要求,∠APM的度数可以是①~⑥中的( )
①10°;②20°;③70°;④80°;⑤160°;⑥170°.

A. ①③⑥
B. ①④⑥
C. ②④⑤
D. ②③⑤
答案:
A【解析】如图
(1),过点$G$作$GH// AB$,令$MN$与$AB$交于$K$。因为$AB// CD$,所以$AB// CD// GH$,所以$\angle FGH=\angle EFG = 30^{\circ}$,$\angle AKG=\angle HGN$。因为$\angle EGN = 40^{\circ}$,$\angle EGF = 90^{\circ}$,所以$\angle FGN = 50^{\circ}$,所以$\angle AKG=\angle HGN = 80^{\circ}$,所以$\angle PKM=\angle AKG = 80^{\circ}$。因为$\angle M = 90^{\circ}$,所以$\angle APM = 180^{\circ}-\angle M-\angle PKM = 10^{\circ}$。如图
(2),过点$G$作$GH// AB$,过点$M$作$KM// AB$。因为$AB// CD$,所以$AB// CD// GH// KM$,所以$\angle FGH=\angle EFG = 30^{\circ}$,$\angle KMG=\angle HGM$,$\angle APM=\angle PMK$。因为$\angle EGN = 40^{\circ}$,$\angle EGF = 90^{\circ}$,所以$\angle KMG=\angle HGM = 180^{\circ}-90^{\circ}-40^{\circ}-30^{\circ}=20^{\circ}$。因为$\angle PMN = 90^{\circ}$,所以$\angle APM=\angle PMK = 90^{\circ}-20^{\circ}=70^{\circ}$。如图
(3),过点$G$作$KG// AB$交$PN$于点$K$。因为$AB// CD$,所以$AB// CD// GK$,所以$\angle FGK=\angle EFG = 30^{\circ}$,$\angle APK=\angle PKG$。因为$\angle EGN = 40^{\circ}$,$\angle EGF = 90^{\circ}$,所以$\angle FGN = 50^{\circ}$,所以$\angle KGN = 80^{\circ}$,所以$\angle NKG = 180^{\circ}-\angle PNM-\angle KGN = 55^{\circ}$,所以$\angle APK=\angle PKG = 180^{\circ}-\angle GKN = 125^{\circ}$,所以$\angle APM=\angle APN+\angle MPN = 170^{\circ}$。故选A。

A【解析】如图
(1),过点$G$作$GH// AB$,令$MN$与$AB$交于$K$。因为$AB// CD$,所以$AB// CD// GH$,所以$\angle FGH=\angle EFG = 30^{\circ}$,$\angle AKG=\angle HGN$。因为$\angle EGN = 40^{\circ}$,$\angle EGF = 90^{\circ}$,所以$\angle FGN = 50^{\circ}$,所以$\angle AKG=\angle HGN = 80^{\circ}$,所以$\angle PKM=\angle AKG = 80^{\circ}$。因为$\angle M = 90^{\circ}$,所以$\angle APM = 180^{\circ}-\angle M-\angle PKM = 10^{\circ}$。如图
(2),过点$G$作$GH// AB$,过点$M$作$KM// AB$。因为$AB// CD$,所以$AB// CD// GH// KM$,所以$\angle FGH=\angle EFG = 30^{\circ}$,$\angle KMG=\angle HGM$,$\angle APM=\angle PMK$。因为$\angle EGN = 40^{\circ}$,$\angle EGF = 90^{\circ}$,所以$\angle KMG=\angle HGM = 180^{\circ}-90^{\circ}-40^{\circ}-30^{\circ}=20^{\circ}$。因为$\angle PMN = 90^{\circ}$,所以$\angle APM=\angle PMK = 90^{\circ}-20^{\circ}=70^{\circ}$。如图
(3),过点$G$作$KG// AB$交$PN$于点$K$。因为$AB// CD$,所以$AB// CD// GK$,所以$\angle FGK=\angle EFG = 30^{\circ}$,$\angle APK=\angle PKG$。因为$\angle EGN = 40^{\circ}$,$\angle EGF = 90^{\circ}$,所以$\angle FGN = 50^{\circ}$,所以$\angle KGN = 80^{\circ}$,所以$\angle NKG = 180^{\circ}-\angle PNM-\angle KGN = 55^{\circ}$,所以$\angle APK=\angle PKG = 180^{\circ}-\angle GKN = 125^{\circ}$,所以$\angle APM=\angle APN+\angle MPN = 170^{\circ}$。故选A。


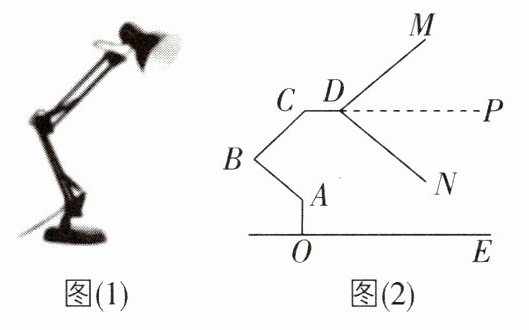
3新考法[2023浙江温州调研,较难]如图(1)是一盏可调节台灯,图(2)为示意图. 固定底座AO⊥OE于点O,BA与CB是分别可绕点A和B旋转的调节杆. 在调节过程中,灯体CD始终保持平行于OE,台灯最外侧光线DM,DN组成的∠MDN始终保持不变. 如图(2),调节台灯使光线DN//BA,此时∠BAO = 130°,且CD的延长线恰好是∠MDN的平分线,则∠MDN = ________。

答案:
$80^{\circ}$【解析】如图,过点$A$作$AF// OE$,过点$B$作$BG// AF$交$DN$于点$H$。因为$AO\perp OE$,所以$\angle AOE = 90^{\circ}$。因为$AF// OE$,所以$\angle OAF = 90^{\circ}$,所以$\angle BAF=\angle BAO-\angle OAF = 40^{\circ}$。因为$BG// AF$,所以$\angle BAF=\angle HBA = 40^{\circ}$。因为$DN// BA$,所以$\angle DHB=\angle HBA = 40^{\circ}$。因为$AF// OE$,$CD// OE$,$BG// AF$,所以$BG// CD$,所以$\angle DHB=\angle PDN = 40^{\circ}$。因为$CD$的延长线恰好是$\angle MDN$的平分线,所以$\angle MDN = 2\angle PDN = 80^{\circ}$。故答案为$80^{\circ}$。
$80^{\circ}$【解析】如图,过点$A$作$AF// OE$,过点$B$作$BG// AF$交$DN$于点$H$。因为$AO\perp OE$,所以$\angle AOE = 90^{\circ}$。因为$AF// OE$,所以$\angle OAF = 90^{\circ}$,所以$\angle BAF=\angle BAO-\angle OAF = 40^{\circ}$。因为$BG// AF$,所以$\angle BAF=\angle HBA = 40^{\circ}$。因为$DN// BA$,所以$\angle DHB=\angle HBA = 40^{\circ}$。因为$AF// OE$,$CD// OE$,$BG// AF$,所以$BG// CD$,所以$\angle DHB=\angle PDN = 40^{\circ}$。因为$CD$的延长线恰好是$\angle MDN$的平分线,所以$\angle MDN = 2\angle PDN = 80^{\circ}$。故答案为$80^{\circ}$。

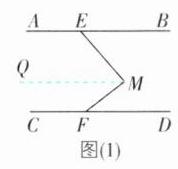
4思想方法|数形结合[2024浙江杭州期末,较难]已知AB//CD,点E,F分别在AB,CD上,M为AB与CD之间一点.
(1)如图(1),试说明∠EMF = ∠BEM + ∠MFD;
(2)如图(2),∠BEM = 40°,MH平分∠EMF,∠BEM的平分线与MH的反向延长线交于点N,若∠N = 30°,求∠MFD的度数;
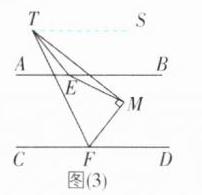
(3)如图(3),FT平分∠MFC,TE平分∠FTM,若∠TMF = 90°,则$\frac{\angle ETF}{\angle MFD}$的值为________。



(1)如图(1),试说明∠EMF = ∠BEM + ∠MFD;
(2)如图(2),∠BEM = 40°,MH平分∠EMF,∠BEM的平分线与MH的反向延长线交于点N,若∠N = 30°,求∠MFD的度数;
(3)如图(3),FT平分∠MFC,TE平分∠FTM,若∠TMF = 90°,则$\frac{\angle ETF}{\angle MFD}$的值为________。



答案:
【解】
(1)如图
(1),过$M$作$MQ// AB$。因为$AB// CD$,所以$AB// MQ// CD$,所以$\angle EMQ=\angle BEM$,$\angle FMQ=\angle MFD$,所以$\angle EMQ+\angle FMQ=\angle BEM+\angle MFD$,所以$\angle EMF=\angle BEM+\angle MFD$。
(2)如图
(2),延长$MH$交$DC$的延长线于点$G$,过点$F$作$FP// MG$。因为$EN$平分$\angle BEM$,$\angle BEM = 40^{\circ}$,所以$\angle BEN=\angle MEN = 20^{\circ}$。因为$MH$平分$\angle EMF$,所以$\angle EMH=\angle FMH$,设$\angle EMH=\angle FMH=\alpha$。因为$AB// CD$,由
(1)易知,$\angle BEN+\angle G=\angle N$,所以$\angle G=\angle N-\angle BEN = 30^{\circ}-20^{\circ}=10^{\circ}$,由
(1)得,$\angle BEM+\angle DFM=\angle EMF$,所以$\angle DFM=\angle EMF-\angle BEM = 2\alpha - 40^{\circ}$。因为$FP// MG$,所以$\angle MFP=\angle FMH=\alpha$,$\angle DFP=\angle G = 10^{\circ}$,所以$\angle DFM=\angle MFP+\angle DFP=\alpha + 10^{\circ}$,所以$2\alpha - 40^{\circ}=\alpha + 10^{\circ}$,解得$\alpha = 50^{\circ}$,所以$\angle MFD=\alpha + 10^{\circ}=60^{\circ}$。
(3)如图
(3),过$T$作$TS// AB$。设$\angle MFD = x^{\circ}$。因为$FT$平分$\angle MFC$,所以$\angle CFT=\angle TFM=\frac{1}{2}(180^{\circ}-\angle MFD)=90^{\circ}-\frac{1}{2}x^{\circ}$。因为$TS// AB$,$AB// CD$,所以$TS// CD$,所以$\angle STF=\angle CFT = 90^{\circ}-\frac{1}{2}x^{\circ}$。由
(1)易知,$\angle STM+\angle MFD=\angle TMF = 90^{\circ}$,所以$\angle STM = 90^{\circ}-x^{\circ}$,所以$\angle FTM=\angle STF-\angle STM=(90^{\circ}-\frac{1}{2}x^{\circ})-(90^{\circ}-x^{\circ})=\frac{1}{2}x^{\circ}$。因为$TE$平分$\angle FTM$,所以$\angle ETF=\frac{1}{2}\angle FTM=\frac{1}{4}x^{\circ}$,所以$\frac{\angle ETF}{\angle MFD}=\frac{1}{4}$。故答案为$\frac{1}{4}$。

【解】
(1)如图
(1),过$M$作$MQ// AB$。因为$AB// CD$,所以$AB// MQ// CD$,所以$\angle EMQ=\angle BEM$,$\angle FMQ=\angle MFD$,所以$\angle EMQ+\angle FMQ=\angle BEM+\angle MFD$,所以$\angle EMF=\angle BEM+\angle MFD$。
(2)如图
(2),延长$MH$交$DC$的延长线于点$G$,过点$F$作$FP// MG$。因为$EN$平分$\angle BEM$,$\angle BEM = 40^{\circ}$,所以$\angle BEN=\angle MEN = 20^{\circ}$。因为$MH$平分$\angle EMF$,所以$\angle EMH=\angle FMH$,设$\angle EMH=\angle FMH=\alpha$。因为$AB// CD$,由
(1)易知,$\angle BEN+\angle G=\angle N$,所以$\angle G=\angle N-\angle BEN = 30^{\circ}-20^{\circ}=10^{\circ}$,由
(1)得,$\angle BEM+\angle DFM=\angle EMF$,所以$\angle DFM=\angle EMF-\angle BEM = 2\alpha - 40^{\circ}$。因为$FP// MG$,所以$\angle MFP=\angle FMH=\alpha$,$\angle DFP=\angle G = 10^{\circ}$,所以$\angle DFM=\angle MFP+\angle DFP=\alpha + 10^{\circ}$,所以$2\alpha - 40^{\circ}=\alpha + 10^{\circ}$,解得$\alpha = 50^{\circ}$,所以$\angle MFD=\alpha + 10^{\circ}=60^{\circ}$。
(3)如图
(3),过$T$作$TS// AB$。设$\angle MFD = x^{\circ}$。因为$FT$平分$\angle MFC$,所以$\angle CFT=\angle TFM=\frac{1}{2}(180^{\circ}-\angle MFD)=90^{\circ}-\frac{1}{2}x^{\circ}$。因为$TS// AB$,$AB// CD$,所以$TS// CD$,所以$\angle STF=\angle CFT = 90^{\circ}-\frac{1}{2}x^{\circ}$。由
(1)易知,$\angle STM+\angle MFD=\angle TMF = 90^{\circ}$,所以$\angle STM = 90^{\circ}-x^{\circ}$,所以$\angle FTM=\angle STF-\angle STM=(90^{\circ}-\frac{1}{2}x^{\circ})-(90^{\circ}-x^{\circ})=\frac{1}{2}x^{\circ}$。因为$TE$平分$\angle FTM$,所以$\angle ETF=\frac{1}{2}\angle FTM=\frac{1}{4}x^{\circ}$,所以$\frac{\angle ETF}{\angle MFD}=\frac{1}{4}$。故答案为$\frac{1}{4}$。



查看更多完整答案,请扫码查看


