第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
5.
- (1)用含有字母的式子表示图中正方形的面积。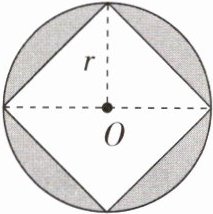
- (2)当$r = 6\text{cm}$时,求出正方形的面积。
- (1)用含有字母的式子表示图中正方形的面积。

- (2)当$r = 6\text{cm}$时,求出正方形的面积。
答案:
$2r^{2}$@@$2r^{2}=2×6^{2}=72(cm^{2})$
6.
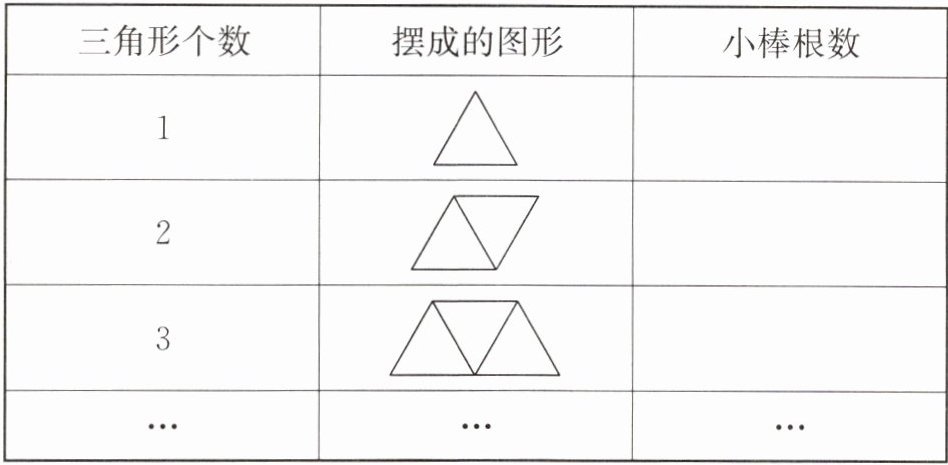
- (1)把表格填完整。你发现了什么规律?用含有字母的式子写出来。
- (2)如果用65根小棒摆三角形,可以摆出多少个三角形?

- (1)把表格填完整。你发现了什么规律?用含有字母的式子写出来。
- (2)如果用65根小棒摆三角形,可以摆出多少个三角形?
答案:
3@@5@@7@@每增加1个三角形,小棒根数就增加2根。$2n + 1$($n$表示三角形个数)@@$2n + 1 = 65$ $n = 32$解析:
(1)从表中图形可以看出,摆1个三角形需要3根小棒,摆2个三角形在1个三角形的基础上增加了2根小棒,一共需要$(3 + 2)$根小棒,摆3个三角形在2个三角形的基础上又增加了2根小棒,一共需要$(3 + 2 + 2)$根小棒……根据这个规律,如果用$n$表示三角形个数,那么摆出$n$个三角形需要用的小棒根数为$(2n + 1)$根。
(2)如果已知摆三角形所用的小棒根数,结合
(1)中的规律,就可以用列方程的方法求出65根小棒可以摆出多少个三角形。
(1)从表中图形可以看出,摆1个三角形需要3根小棒,摆2个三角形在1个三角形的基础上增加了2根小棒,一共需要$(3 + 2)$根小棒,摆3个三角形在2个三角形的基础上又增加了2根小棒,一共需要$(3 + 2 + 2)$根小棒……根据这个规律,如果用$n$表示三角形个数,那么摆出$n$个三角形需要用的小棒根数为$(2n + 1)$根。
(2)如果已知摆三角形所用的小棒根数,结合
(1)中的规律,就可以用列方程的方法求出65根小棒可以摆出多少个三角形。
7. 列方程解决问题。
- (1)学校鼓号队有24人,相当于舞蹈队人数的$\frac{2}{3}$,舞蹈队有多少人?
- (2)甲、乙两只松鼠各采摘了多少个松果?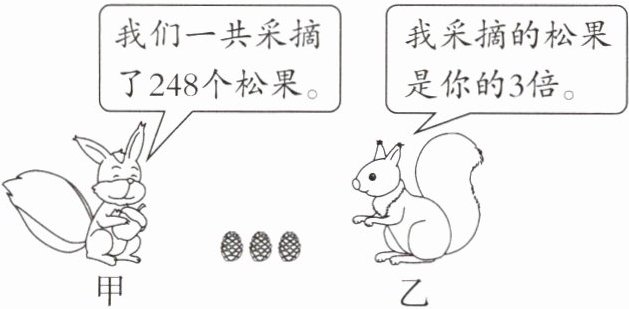
- (1)学校鼓号队有24人,相当于舞蹈队人数的$\frac{2}{3}$,舞蹈队有多少人?
- (2)甲、乙两只松鼠各采摘了多少个松果?

答案:
解:设舞蹈队有$x$人。$\frac{2}{3}x = 24$ $x = 36$@@解:设甲松鼠采摘了$x$个松果,则乙松鼠采摘了$3x$个松果。$x + 3x = 248$ $x = 62$ $62×3 = 186$(个)
24×( )=8 ( )×5.4=2.7 25%×( )=1 ( )+7.8=10
答案:
$\frac{1}{3}$@@$\frac{1}{2}$@@4@@2.2
查看更多完整答案,请扫码查看


