第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 填一填。
将圆柱通过下图所示的方法等分、切割和拼接,可以把圆柱转化成近似的 __________。拼接成的立体图形的体积与圆柱的 __________ 相等。
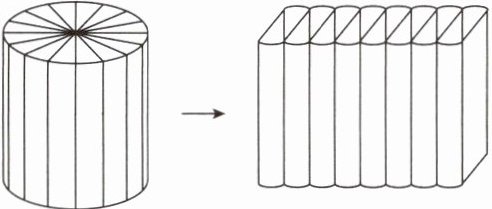

圆柱的体积公式:$V=$ __________ = __________
将圆柱通过下图所示的方法等分、切割和拼接,可以把圆柱转化成近似的 __________。拼接成的立体图形的体积与圆柱的 __________ 相等。


圆柱的体积公式:$V=$ __________ = __________
答案:
长方体@@体积@@圆柱的底面积@@圆柱的高@@Sh@@πr²h
2. 选一选。(将正确答案的序号填在括号里)
(1)下列说法正确的是( )。
A. 正方体、长方体和圆柱的体积都可以用“底面积×高”计算
B. 一个圆柱的高不变,底面半径扩大到原来的 3 倍,体积也扩大到原来的 3 倍
C. 两个圆柱的表面积相等,它们的体积也一定相等
D. 求一个圆柱的容积也就是求这个圆柱的体积
(2)将一个棱长是 8dm 的正方体木料削成一个最大的圆柱,圆柱的体积是( )$dm^{3}$。
A. 50.24 B. 200.96 C. 401.92 D. 1607.68
(1)下列说法正确的是( )。
A. 正方体、长方体和圆柱的体积都可以用“底面积×高”计算
B. 一个圆柱的高不变,底面半径扩大到原来的 3 倍,体积也扩大到原来的 3 倍
C. 两个圆柱的表面积相等,它们的体积也一定相等
D. 求一个圆柱的容积也就是求这个圆柱的体积
(2)将一个棱长是 8dm 的正方体木料削成一个最大的圆柱,圆柱的体积是( )$dm^{3}$。
A. 50.24 B. 200.96 C. 401.92 D. 1607.68
答案:
A@@C
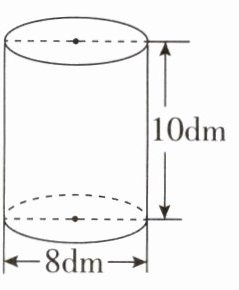
3. 计算下面各圆柱的体积。
(1)
(2)
(1)

(2)

答案:
12.56×30 = 376.8(cm³)@@3.14×(8÷2)²×10 = 502.4(dm³)
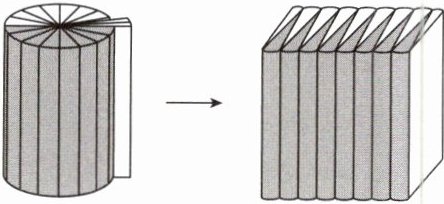
4. 易错题 把高是 10cm 的圆柱按下图切开,拼成近似的长方体,表面积增加了 60$cm^{2}$。圆柱的体积是多少立方厘米?

答案:
60÷2÷10 = 3(cm)
3.14×3²×10 = 282.6(cm³)
解析:将圆柱沿半径切开拼成近似的长方体后,表面积增加,增加的部分是长方体左右的两个面,也就是底面半径与高的乘积的2倍,根据已知增加的表面积和圆柱的高,可以求出圆柱的底面半径,再根据圆柱的体积公式V = Sh就可以求出圆柱的体积。
3.14×100= 3³= (2+2)³= (18-9)²= (5×2)³=
答案:
314@@27@@64@@81@@1000
查看更多完整答案,请扫码查看


