《2025年学霸高考黑题数学人教版》

变式训练3. (2025·山西太原月考)
已知正方体ABCD - A₁B₁C₁D₁的棱长为2，E，F分别是棱AA₁，A₁D₁的中点，点P为底面ABCD内(包括边界)的一动点，若直线D₁P与平面BEF无公共点，则点P的轨迹长度为(B)

A.√2
B.√5
C.2
D.√3

答案：
变式训练3.B解析:以点D为坐标原点，$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{DD₁}$的方向分别为x,y,z轴的正方向，建立如图所示的空间直角坐标系，则$B(2,2,0)$，$E(2,0,1)$，$F(1,0,2)$，$D₁(0,0,2)$，设点$P(a,b,0)$，则$\overrightarrow{BE}=(0,-2,1)$，$\overrightarrow{EF}=(-1,0,1)$，$\overrightarrow{D₁P}=(a,b,-2)$。设平面BEF的法向量为$\boldsymbol{m}=(x,y,z)$，由$\begin{cases}\boldsymbol{m}·\overrightarrow{BE}=-2y + z = 0\\\boldsymbol{m}·\overrightarrow{EF}=-x + z = 0\end{cases}$取$z = 2$，可得$x = 2,y = 1$，所以$\boldsymbol{m}=(2,1,2)$为平面BEF的一个法向量。由题意可知，$D₁P//$平面BEF，则$\overrightarrow{D₁P}·\boldsymbol{m}=2a + b - 4 = 0$，令$b = 0$，可得$a = 2$；令$b = 2$，可得$a = 1$，所以点P的轨迹为线段，且交AD于点$A(2,0,0)$，交BC于点$M(1,2,0)$，所以点P的轨迹长度为$AM=\sqrt{AB^2 + BM^2}=\sqrt{2^2 + 1^2}=\sqrt{5}$。
　　　　　　　

变式训练4. (2025·河南驻马店月考)
如图，在棱长为√6的正方体ABCD - A₁B₁C₁D₁中，点P是平面A₁BC₁内的一个动点，当PB₁ + PD = 2 + √10时，点P的轨迹长度是(D)

A.6π
B.4π
C.2√3π
D.2√2π

答案：
变式训练4.D解析:如图,设$B₁D\cap$平面$A₁BC₁ = E$，连接PE,BE，$B₁D₁,BD$。因为$A₁B = BC₁ = A₁C₁ = 2\sqrt{3}$，$A₁B₁ = BB₁ = B₁C₁$，所以三棱锥$B₁ - A₁BC₁$为正三棱锥。因为$DD₁\perp$平面$A₁B₁C₁D₁$，$A₁C₁\subset$平面$A₁B₁C₁D₁$，所以$DD₁\perp A₁C₁$。因为$A₁C₁\perp B₁D₁$，$DD₁\cap B₁D₁ = D₁$，所以$A₁C₁\perp$平面$BDD₁B₁$。又$B₁D\subset$平面$BDD₁B₁$，所以$B₁D\perp A₁C₁$。同理可证$B₁D\perp A₁B$，又$A₁C₁\cap A₁B = A₁$，$A₁C₁,A₁B\subset$平面$A₁BC₁$，所以$B₁D\perp$平面$A₁BC₁$，则E为正三角形$A₁BC₁$的中心，则$BE = 2$，所以$B₁E = \sqrt{BB₁² - BE²} = \sqrt{2}$；因为$B₁D = 3\sqrt{2}$，所以$DE = B₁D - B₁E = 2\sqrt{2}$；因为$B₁D\perp$平面$A₁BC₁$，$PE\subset$平面$A₁BC₁$，所以$PE\perp B₁D$，即$B₁E\perp PE$，$DE\perp PE$；因为$PB₁ + PD = 2 + \sqrt{10}$，所以$\sqrt{PE² + 8} + \sqrt{PE² + 2} = 2 + \sqrt{10}$。因为$PE ＞ 0$，解得$PE = \sqrt{2}$，所以点P的轨迹是半径为√2的圆，所以点P的轨迹长度是$2\sqrt{2}\pi$。
　　　　　　　

变式训练5. (2025·安徽合肥月考)
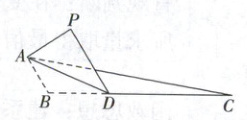
如图，在△ABC中，AB⊥BC，BC = 3AB = 3，D是BC上一点，且BD = 1，将△BAD沿AD翻折，使得点B与点P重合，当动点P在平面ADC上的射影在△ADC内部及边界上时，动点P的轨迹长度为(A)

A.$\frac{\sqrt{2}}{12}\pi$
B.$\frac{\sqrt{2}}{8}\pi$
C.$\frac{\sqrt{2}}{6}\pi$
D.$\frac{\sqrt{2}}{4}\pi$

答案：
变式训练5.A解析:如图①所示,过点B作$BF\perp AD$，分别交AD,AC于点E,F，则动点P在平面ADC上的射影轨迹为线段EF。设当P与$P₁$重合时，有$P₁E\perp EF$；当P与$P₂$重合时，有$P₂F\perp EF$，则由$PE = BE$为定长，可知动点P的轨迹是以E为圆心，以BE为半径且圆心角为$\angle P₁EP₂$的圆弧。在$\triangle ABC$所在平面建立如图②所示的平面直角坐标系，则$A(0,1)$，$D(1,0)$，$C(3,0)$，$E(\frac{1}{2},\frac{1}{2})$，直线$BE:y = x$，直线$AC:y = -\frac{1}{3}x + 1$，联立方程组$\begin{cases}y = x\\y = -\frac{1}{3}x + 1\end{cases}$解得$\begin{cases}x = \frac{3}{4}\\y = \frac{3}{4}\end{cases}$即$F(\frac{3}{4},\frac{3}{4})$，则$EF = \frac{\sqrt{2}}{4}$。又由$BE = \frac{\sqrt{2}}{2}$，可得$\cos\angle P₂EF = \frac{EF}{BE} = \frac{1}{2}$，所以$\angle P₂EF = \frac{\pi}{3}$，所以$\angle P₁EP₂ = \frac{\pi}{6}$，所以动点P的轨迹长度为$\frac{\sqrt{2}}{2}×\frac{\pi}{6}=\frac{\sqrt{2}\pi}{12}$。
　　 　　

变式训练6. (多选)(2025·山东日照期末)
如图，已知正方体ABCD - A₁B₁C₁D₁的棱长为2，M是DD₁的中点，N为正方形ABCD所在平面内一动点，则下列结论正确的是(ABD)

A.若N到直线BB₁与直线DC的距离相等，则N的轨迹为抛物线
B.若MN = 2，则MN的中点的轨迹所围成图形的面积为$\frac{3\pi}{4}$
C.若直线MN与平面ABCD所成的角为60°，则N的轨迹为椭圆
D.若直线D₁N与直线AB所成的角为60°，则N的轨迹为双曲线

答案：
变式训练6.ABD解析:对于A，$BB₁\perp$平面ABCD，NB即为N到直线$BB₁$的距离，在平面ABCD内，点N到定点B的距离与到定直线DC的距离相等，所以点N的轨迹就是以B为焦点，DC为准线的抛物线，故A正确；对于B，若$MN = 2$，则$ND = \sqrt{3}$，可得MN中点的轨迹为以MD中点为圆心，$\frac{\sqrt{3}}{2}$为半径，且平行于平面ABCD的圆，其面积为$\pi×(\frac{\sqrt{3}}{2})^2 = \frac{3}{4}\pi$，故B正确；对于C，MN与平面ABCD所成的角为$\angle MND$，则$\angle MND = \frac{\pi}{3}$，可得$DN = \frac{\sqrt{3}}{3}$，所以点N的轨迹为以D为圆心，$\frac{\sqrt{3}}{3}$为半径的圆，故C错误；对于D，如图，建立空间直角坐标系，$D(0,0,0)$，$D₁(0,0,2)$，$A(2,0,0)$，$B(2,2,0)$，设$N(x,y,0)$，则$\overrightarrow{D₁N}=(x,y,-2)$，$\overrightarrow{AB}=(0,2,0)$。因为$\cos60°=\frac{\vert\overrightarrow{D₁N}·\overrightarrow{AB}\vert}{\vert\overrightarrow{D₁N}\vert\vert\overrightarrow{AB}\vert}=\frac{2y}{\sqrt{x^2 + y^2 + 4}×2}=\frac{1}{2}$，化简得$3y^2 - x^2 = 4$，即$\frac{y^2}{4}-\frac{x^2}{4}=1$，所以N的轨迹为双曲线，故D正确。
　　　　　　　　

变式训练7. (2025·陕西咸阳模拟)
在正方体ABCD - A₁B₁C₁D₁中，E为A₁D₁的中点，F为底面ABCD上一动点，EF与底面ABCD所成的角为θ，若sinθ - cosθ = $\frac{\sqrt{3} - 1}{2}$，且该正方体的外接球的体积为4√3π，则动点F的轨迹长度为______。

答案：
变式训练7.$\frac{4\sqrt{3}\pi}{9}$解析:如图①所示，取AD的中点H，连接EH，则$EH// AA₁$，在正方体ABCD−A₁B₁C₁D₁中，$AA₁\perp$底面ABCD，所以$EH\perp$底面ABCD，所以$\angle EFH$为$EF$与底面ABCD所成的角$\theta$。因为$\sin\theta - \cos\theta = \frac{\sqrt{3} - 1}{2}$，所以$\theta = \angle EFH = \frac{\pi}{3}$。设正方体的棱长为$a$，因为正方体的外接球的体积为$4\sqrt{3}\pi$，所以$\frac{4}{3}\pi×(\frac{\sqrt{3}}{2}a)^3 = 4\sqrt{3}\pi$，解得$a = 2$，所以$EH = AA₁ = a = 2$，可得$HF = \frac{2\sqrt{3}}{3}$，所以点F的轨迹为以H为圆心，$\frac{2\sqrt{3}}{3}$为半径的圆在正方形ABCD区域内的部分$\overset{\frown}{MG}$，如图②所示，$HG = HM = \frac{2\sqrt{3}}{3}$，所以$\cos\angle AHG = \frac{\frac{\sqrt{3}}{3}}{\frac{2\sqrt{3}}{3}} = \frac{\sqrt{3}}{2}$，则$\angle AHG = \frac{\pi}{6}$，根据对称性，可得$\angle DHM = \frac{\pi}{6}$，所以$\angle MHG = \pi - 2×\frac{\pi}{6} = \frac{2\pi}{3}$，故动点F的轨迹长度为$\frac{2\pi}{3}×\frac{2\sqrt{3}}{3}=\frac{4\sqrt{3}\pi}{9}$。
　　　　　 　　

变式训练 8.（2025·广东广州模拟）在正三棱锥$P - ABC$中，$PA = PB = PC = 3\sqrt{2}$，$AB = 6$，点$D$在$\triangle ABC$内部运动（包括边界），点$D$到棱$PA$，$PB$，$PC$的距离分别记为$d_{1}$，$d_{2}$，$d_{3}$，且$d_{1}^{2}+d_{2}^{2}+d_{3}^{2}=20$，则点$D$运动路径的长度为______.

答案： \( 2\sqrt{3}\pi \)