2025年学霸高考黑题数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学霸高考黑题数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第105页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
典型例题 1. (2025·辽宁沈阳二模)古希腊数学家阿波罗尼斯采用平面切割圆锥面的方法来研究圆锥曲线,如图①,设圆锥轴截面的顶角为 $2\alpha$,用一个平面 $\Gamma$ 去截该圆锥面,随着圆锥的轴和 $\Gamma$ 所成角 $\beta$ 的变化,截得的曲线的形状也不同。据研究,曲线的离心率为 $e = \frac{\cos \beta}{\cos \alpha}$,比如,当 $\alpha = \beta$ 时,$e = 1$,此时截得的曲线是抛物线。如图②,在底面半径为 $1$,高为 $2\sqrt{2}$ 的圆锥 $SO$ 中,$AB$,$CD$ 是底面圆 $O$ 上互相垂直的直径,$E$ 是母线 $SC$ 上一点,$SE = 2EC$,平面 $ABE$ 截该圆锥面所得的曲线的离心率为( )
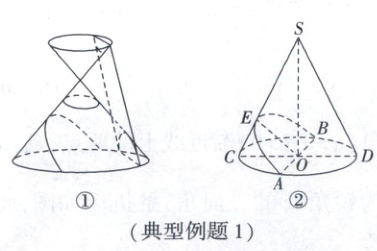
A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{\sqrt{3}}{2}$
D.$\frac{2\sqrt{3}}{3}$

A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{\sqrt{3}}{2}$
D.$\frac{2\sqrt{3}}{3}$
答案:
典型例题1.C解析:由题意得$\angle OSC = \alpha$,$\angle EOS = \beta$,则$\angle SCO = 90^{\circ} - \alpha$,$\angle EOC = 90^{\circ} - \beta$,所以$e = \frac{\cos \beta}{\cos \alpha} = \frac{\sin \angle EOC}{\sin \angle SCO}$。在$\triangle SOC$中,$SE = 2EC$,$SO = 2\sqrt{2}$,$CO = 1$,且$SO \perp OC$,则$SC = \sqrt{SO^{2} + OC^{2}} = 3$,所以$EC = 1$,$\overrightarrow{OE} = \overrightarrow{OS} + \overrightarrow{SE} = \overrightarrow{OS} + \frac{2}{3}\overrightarrow{SC} = \overrightarrow{OS} + \frac{2}{3}(\overrightarrow{OC} - \overrightarrow{OS}) = \frac{2}{3}\overrightarrow{OC} + \frac{1}{3}\overrightarrow{OS}$,则$|\overrightarrow{OE}|^{2} = (\frac{2}{3}\overrightarrow{OC} + \frac{1}{3}\overrightarrow{OS})^{2} = \frac{4}{9}\overrightarrow{OC}^{2} + \frac{4}{9}\overrightarrow{OC} · \overrightarrow{OS} + \frac{1}{9}\overrightarrow{OS}^{2} = \frac{4}{3}$,所以$OE = \frac{2\sqrt{3}}{3}$。
由正弦定理得$\frac{EC}{\sin \angle EOC} = \frac{EO}{\sin \angle SCO}$,即$\frac{\sin \angle EOC}{\sin \angle SCO} = \frac{EC}{EO} = \frac{\sqrt{3}}{2}$。
由正弦定理得$\frac{EC}{\sin \angle EOC} = \frac{EO}{\sin \angle SCO}$,即$\frac{\sin \angle EOC}{\sin \angle SCO} = \frac{EC}{EO} = \frac{\sqrt{3}}{2}$。
变式训练 1. (2025·湖南长沙一中模拟)用平面 $\alpha$ 截圆柱面,圆柱的轴与平面 $\alpha$ 所成的角记为 $\theta$,当 $\theta$ 为锐角时,圆柱面的截线是一个椭圆,数学家当德兰创立的双球模型证明了上述结论。如图所示,将两个大小相同的球嵌入圆柱内,使它们分别位于平面 $\alpha$ 的上方和下方,并且与圆柱面和平面 $\alpha$ 均相切,切点分别为 $F_1$,$F_2$。下列关于截口曲线的椭圆的结论中不正确的有(
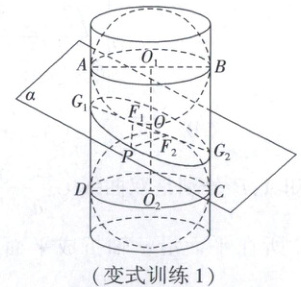
A.椭圆的短轴长与嵌入圆柱的球的直径相等
B.椭圆的长轴长与嵌入圆柱的两球的球心距 $|O_1O_2|$ 相等
C.所得椭圆的离心率 $e = \cos \theta$
D.其中 $G_1G_2$ 为椭圆长轴,$R$ 为球 $O_1$ 的半径,有 $R = |AG_1| · \tan \frac{\theta}{2}$
D
)
A.椭圆的短轴长与嵌入圆柱的球的直径相等
B.椭圆的长轴长与嵌入圆柱的两球的球心距 $|O_1O_2|$ 相等
C.所得椭圆的离心率 $e = \cos \theta$
D.其中 $G_1G_2$ 为椭圆长轴,$R$ 为球 $O_1$ 的半径,有 $R = |AG_1| · \tan \frac{\theta}{2}$
答案:
变式训练1.D解析:设$P$为截口曲线的椭圆的一点,如图,过点$P$作线段$EF$分别与球$O_1$,$O_2$切于点$F$,$E$,故有$|PF_1| + |PF_2| = |PF| + |PE| = |EF| = |O_1O_2|$,由椭圆定义可知,该椭圆以$F_1$,$F_2$为焦点,$|O_1O_2|$为长轴长,故B正确。
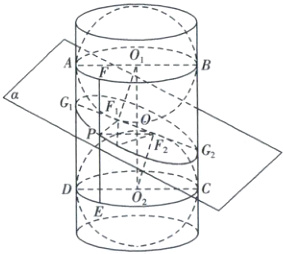
设椭圆长半轴长为$a$,半焦距为$c$,设$O$为$O_1O_2$的中点,$PF_1$与球$O_1$切于点$F_1$,$O_1F_1 \perp \alpha$,$O_1F_1 \subset \alpha$,故$O_1F_1 \perp OF_1$,有$|O_1F_1|^{2} = |OO_1|^{2} - |OF_1|^{2} = a^{2} - c^{2} = b^{2}$,则$2b = 2|O_1F_1|$,即椭圆的短轴长与嵌入圆柱的球的直径相等,故A正确。
由题意可得$\theta = \angle O_1OF_1$,则$e = \frac{c}{a} = \frac{|OF_1|}{|OO_1|} = \cos \theta$,故C正确。
由题意知$|AG_1| = |F_1G_1|$,$\theta = \angle O_1OF_1 = \angle AOF_1$(这是因为$\angle O_1OF_1 + \angle OOF_1 = \angle AOF_1 + \angle O_1OF_1 = \frac{\pi}{2}$),则$\frac{\theta}{2} = \frac{1}{2}\angle AOF_1 = \angle G_1OF_1$,故$\tan \frac{\theta}{2} = \frac{|F_1G_1|}{R} = \frac{|AG_1|}{R}$,即$R = \frac{|AG_1|}{\tan \frac{\theta}{2}}$,故D错误。
变式训练1.D解析:设$P$为截口曲线的椭圆的一点,如图,过点$P$作线段$EF$分别与球$O_1$,$O_2$切于点$F$,$E$,故有$|PF_1| + |PF_2| = |PF| + |PE| = |EF| = |O_1O_2|$,由椭圆定义可知,该椭圆以$F_1$,$F_2$为焦点,$|O_1O_2|$为长轴长,故B正确。

设椭圆长半轴长为$a$,半焦距为$c$,设$O$为$O_1O_2$的中点,$PF_1$与球$O_1$切于点$F_1$,$O_1F_1 \perp \alpha$,$O_1F_1 \subset \alpha$,故$O_1F_1 \perp OF_1$,有$|O_1F_1|^{2} = |OO_1|^{2} - |OF_1|^{2} = a^{2} - c^{2} = b^{2}$,则$2b = 2|O_1F_1|$,即椭圆的短轴长与嵌入圆柱的球的直径相等,故A正确。
由题意可得$\theta = \angle O_1OF_1$,则$e = \frac{c}{a} = \frac{|OF_1|}{|OO_1|} = \cos \theta$,故C正确。
由题意知$|AG_1| = |F_1G_1|$,$\theta = \angle O_1OF_1 = \angle AOF_1$(这是因为$\angle O_1OF_1 + \angle OOF_1 = \angle AOF_1 + \angle O_1OF_1 = \frac{\pi}{2}$),则$\frac{\theta}{2} = \frac{1}{2}\angle AOF_1 = \angle G_1OF_1$,故$\tan \frac{\theta}{2} = \frac{|F_1G_1|}{R} = \frac{|AG_1|}{R}$,即$R = \frac{|AG_1|}{\tan \frac{\theta}{2}}$,故D错误。
查看更多完整答案,请扫码查看


