《2025年学霸高考黑题数学人教版》

变式训练4. (2025·浙江温州月考)已知一圆锥底面圆的直径为3，圆锥的高为$\frac{3\sqrt{3}}{2}$，在该圆锥内放置一个棱长为$a$的正四面体，并且正四面体在该几何体内可以任意转动，则$a$的最大值为(B)

A.3
B.$\sqrt{2}$
C.$\frac{9}{2}(\sqrt{3}-\sqrt{2})$
D.$\frac{3\sqrt{2}}{2}$

答案：
变式训练4.B 解析:依题意，四面体可以在圆锥内任意转动，故该四面体内接于圆锥的内切球，设球心为P,球P的半径为r,圆锥的轴截面上球与圆锥母线的切点为Q,圆锥的轴截面如图①:

则$OA = OB = \frac{3}{2}$,$MO = \frac{3\sqrt{3}}{2}$,所以$MA = MB = \sqrt{MO^{2} + OA^{2}} = 3$,所以$\triangle MAB$为等边三角形,$S_{\triangle MAB} = \frac{1}{2}MO · AB = \frac{1}{2} × \frac{3\sqrt{3}}{2} × 3 = \frac{9\sqrt{3}}{4}$.由等面积法可得$S_{\triangle MAB} = \frac{1}{2} · r · 3AB = \frac{9r}{2} = \frac{9\sqrt{3}}{4}$,解得$r = \frac{\sqrt{3}}{2}$,即四面体的外接球的半径为$r = \frac{\sqrt{3}}{2}$.另正四面体可以从正方体中截得，如图②:

从图中可以得到，当正四面体的棱长为a时，截得它的正方体的棱长为$\frac{\sqrt{2}}{2}a$,而正四面体的四个顶点都在正方体上,故正四面体的外接球即为截得它的正方体的外接球,所以$2r = \sqrt{3} × \frac{\sqrt{2}}{2}a = \frac{\sqrt{6}}{2}a$,所以$a = \sqrt{2}$.即a的最大值为$\sqrt{2}$.

变式训练5. (2025·重庆一中模拟)棱长为$4\sqrt{3}$的正四面体内切一球，然后在正四面体和该球形成的空隙处各放入一个小球，则这样一个小球的体积最大为(D)

A.$\frac{8\sqrt{2}\pi}{3}$
B.$\frac{4\sqrt{2}\pi}{3}$
C.$2\pi$
D.$\frac{\sqrt{2}}{3}\pi$

答案：
变式训练5.D 解析:如图，由题意知小球和正四面体A - BCD的三个侧面以及内切球都相切时半径最大，设内切球球心为O,半径为R，空隙处的最大球球心为$O_{1}$,半径为r,由正四面体结构特征可知G为$\triangle BCD$的中心,$AG \perp$平面BCD,设E为CD中点，球O和球$O_{1}$分别与面ACD相切于F和H.易得$BE = \sqrt{(4\sqrt{3})^{2} - (2\sqrt{3})^{2}} = 6$,$BG = \frac{2}{3}BE = 4$,$AG = \sqrt{(4\sqrt{3})^{2} - 4^{2}} = 4\sqrt{2}$,由$V_{A - BCD} = V_{O - BCD} + V_{O - ABC} + V_{O - ACD} + V_{O - ABD}$可得$R = \frac{3V_{A - BCD}}{S_{O - BCD} + S_{O - ABC} + S_{O - ACD} + S_{O - ABD}} = \frac{1}{3} × (\frac{1}{2} × 4\sqrt{3} × 6) × 4\sqrt{2} = 16\sqrt{6}$,$S_{\triangle BCD} = S_{\triangle ABC} = S_{\triangle ABD} = S_{\triangle ACD} = \frac{1}{2} × 4\sqrt{3} × 6 = 12\sqrt{3}$,故$R = \frac{3 × 16\sqrt{6}}{4 × 12\sqrt{3}} = \sqrt{2}$,$AO_{1} = AG - G_{0} = 4\sqrt{2} - 2\sqrt{2} - r = 2\sqrt{2} - r$,$AO = AG - G_{0} = 4\sqrt{2} - \sqrt{2} = 3\sqrt{2}$.

又由$\triangle AO_{1}H$和$\triangle AOF$相似，可得$\frac{AO_{1}}{AO} = \frac{O_{1}H}{OF}$,即$\frac{2\sqrt{2} - r}{3\sqrt{2}} = \frac{r}{\sqrt{2}}$,解得$r = \frac{\sqrt{2}}{2}$,即空隙处的最大球的半径为$\frac{\sqrt{2}}{2}$.所以空隙处的最大球的体积为$\frac{4}{3}\pi(\frac{\sqrt{2}}{2})^{3} = \frac{\sqrt{2}\pi}{3}$.

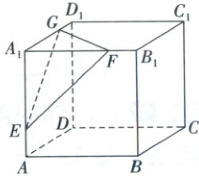
变式训练6. (2025·河南信阳模拟)如图，现有棱长为4cm的正方体玉石缺失了一个角，缺失部分为正三棱锥$A_{1}-EFG$，且$E$，$F$，$G$分别为棱$A_{1}A$，$A_{1}B_{1}$，$A_{1}D_{1}$上离$A_{1}$最远的四等分点，若将该玉石打磨成一个球形饰品，则该球形饰品的半径的最大值为$\frac{9 - 3\sqrt{3}}{2}$cm.

答案：
变式训练6.$\frac{9 - 3\sqrt{3}}{2}$ 解析:由题意可得$A_{1}E = A_{1}F = A_{1}G = 4 × \frac{3}{4} = 3(cm)$,所以$\triangle EFG$为等边三角形，设$\triangle EFG$的中心为T,如图①,连接$A_{1}C_{1}$,$B_{1}D_{1}$,$ET$,则$ET \perp GF$.因为$EA_{1} \perp$平面$A_{1}GF$,$GFC \subset$平面$A_{1}GF$,所以$EA_{1} \perp GF$.又$ET \cap EA_{1} = E$,$ET$,$EA_{1} \subset$平面$A_{1}ET$,所以$GF \perp$平面$A_{1}ET$,$A_{1}T \subset$平面$A_{1}ET$,所以$GF \perp A_{1}T$,同理可证$GE \perp A_{1}T$,$GF$,$GE \subset$平面$EFG$,$GF \cap GE = G$,所以$A_{1}T \perp$平面$EFG$.因为$\frac{A_{1}G}{A_{1}D_{1}} = \frac{A_{1}F}{A_{1}B_{1}} = \frac{3}{4}$,所以$FG // B_{1}D_{1}$.又$A_{1}C_{1} \perp B_{1}D_{1}$,所以$FG \perp A_{1}C_{1}$,又$CC_{1} \perp FG$,$CC_{1} \cap A_{1}C_{1} = C_{1}$,$CC_{1}$,$A_{1}C_{1} \subset$平面$A_{1}C_{1}C$,所以$FG \perp$平面$A_{1}C_{1}C$.因为$A_{1}C \subset$平面$A_{1}C_{1}C$,所以$FG \perp A_{1}C$,同理证明$EG \perp A_{1}C$,又$GF$,$GE \subset$平面$EFG$,$GF \cap GE = G$,所以$A_{1}C \perp$平面$EFG$,所以$A_{1}$,$T$,$C$三点共线，设点$A_{1}$到平面$EFG$的距离为$d = A_{1}T$,而$EF = EG = FG = \sqrt{3^{2} + 3^{2}} = 3\sqrt{2}(cm)$,$S_{\triangle EFG} = \frac{1}{2} × 3\sqrt{2} × 3\sqrt{2} × \sin 60^{\circ} = \frac{9\sqrt{3}}{2}(cm^{2})$.由$V_{A_{1} - EFG} = \frac{1}{3} × \frac{1}{2} × 3 × 3 × 3 = \frac{1}{3} × \frac{9\sqrt{3}}{2}d$,解得$d = \sqrt{3}cm$,即$A_{1}T = \sqrt{3}cm$,又$A_{1}C = 4\sqrt{3}cm$,所以$TC = 3\sqrt{3}cm$.因为$2\sqrt{3} - \sqrt{3} = \sqrt{3} ＜ 2$,所以该球不是正方体的内切球.设$A_{1}C_{1}$交$FG$于点$M$,连接$EM$,$AC$,$A_{1}C$.
　　
由对称性可得球的球心位于线段$TC$上，且该球与平面$EFG$相切，与平面$ABCD$相切，截面如图②，设球心为$O$，球的半径为$R$，则$OT = R$，$\frac{OC}{R} = \frac{A_{1}C}{A_{1}A} = \sqrt{3}$，故$\sqrt{3}R = R + \sqrt{3}R$，所以$R = \frac{9 - 3\sqrt{3}}{2}cm$，所以所求球形饰品的半径的最大值为$\frac{9 - 3\sqrt{3}}{2}cm$.

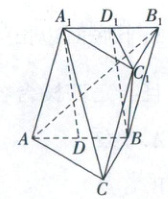
变式训练7. (2025·广东深圳中学模拟)如图所示，斜三棱柱$ABC - A_{1}B_{1}C_{1}$中，$D$为$AB$的中点，$D_{1}$为$A_{1}B_{1}$的中点，平面$ABC\perp$平面$ABB_{1}A_{1}$.
(1)求证：直线$A_{1}C//$平面$BC_{1}D_{1}$；
(2)若三角形$A_{1}B_{1}C_{1}$是等边三角形且边长为2，侧棱$AA_{1}=\frac{\sqrt{6}}{2}$，且异面直线$BC_{1}$与$AB_{1}$互相垂直，求异面直线$A_{1}D$与$BC_{1}$所成角的正切值；
(3)若$AB = 8$，$AC = BC = 5$，$\cos\angle A_{1}AB=\frac{\sqrt{13}}{4}$，若三棱柱$ABC - A_{1}B_{1}C_{1}$有内切球，求三棱柱$ABC - A_{1}B_{1}C_{1}$的体积.

答案：
变式训练7.
(1)证明：如图①，连接$B_{1}C$交$BC_{1}$于点$E$，连接$D_{1}E$，

所以$E$为$B_{1}C$的中点，而$D_{1}$为$A_{1}B_{1}$的中点，由中位线定理得$A_{1}C // D_{1}E$.因为$A_{1}C \not\subset$平面$BC_{1}D_{1}$，$D_{1}E \subset$平面$BC_{1}D_{1}$，故$A_{1}C //$平面$BC_{1}D_{1}$.
(2)解：由题意得$A_{1}D // BD_{1}$，所以$\angle C_{1}BD_{1}$为异面直线$A_{1}D$与$BC_{1}$所成角。因为$\triangle A_{1}B_{1}C_{1}$为正三角形，$D_{1}$为$A_{1}B_{1}$的中点，所以$C_{1}D_{1} \perp A_{1}B_{1}$.又因为平面$A_{1}B_{1}C_{1} \perp$平面$A_{1}ABB_{1}$，平面$A_{1}B_{1}C_{1} \cap$平面$A_{1}ABB_{1} = A_{1}B_{1}$，$C_{1}D_{1} \subset$平面$A_{1}B_{1}C_{1}$，所以$C_{1}D_{1} \perp$平面$A_{1}ABB_{1}$，而$BD_{1} \subset$平面$A_{1}ABB_{1}$，故$C_{1}D_{1} \perp BD_{1}$，$C_{1}D_{1} \perp AB_{1}$.又因为$AB_{1} \perp BC_{1}$，$C_{1}D_{1} \cap BC_{1} = C_{1}$，$C_{1}D_{1}$，$BC_{1} \subset$平面$BC_{1}D_{1}$，所以$AB_{1} \perp$平面$BC_{1}D_{1}$，而$BD_{1} \subset$平面$BC_{1}D_{1}$，则$AB_{1} \perp BD_{1}$，设$AF = \frac{2}{3}BD_{1}$，$AF = \frac{2}{3}AB_{1}$，则$BD_{1}^{2} = \frac{3}{2} + 4 + 2\sqrt{6}\cos\angle A_{1}B_{1}B$，$AB_{1}^{2} = \frac{3}{2} + 4 + 2\sqrt{6}\cos\angle A_{1}B_{1}B$，故由勾股定理得$AF^{2} + FB^{2} = AB_{1}^{2}$，则$\frac{4}{9}(\frac{5}{2} - \sqrt{6}\cos\angle A_{1}B_{1}B) + \frac{4}{9}(\frac{11}{2} + 2\sqrt{6}\cos\angle A_{1}B_{1}B) = 4$，解得$\cos\angle A_{1}B_{1}B = \frac{1}{\sqrt{6}}$，故$BD_{1} = \frac{\sqrt{6}}{2}$，则$\tan\angle C_{1}BD_{1} = \frac{C_{1}D_{1}}{BD_{1}} = \frac{\sqrt{3}}{\frac{\sqrt{6}}{2}} = \sqrt{2}$，即异面直线$A_{1}D$与$BC_{1}$所成角的正切值为$\sqrt{2}$.
(3)解：我们首先来证明三余弦定理，我们记$A$为平面$\alpha$上方的一点，过$A$的斜线$AB$在平面$\alpha$上的射影为$BO$，$BC$为平面$\alpha$内的任意一条直线，记$\beta$为斜线角，$\alpha_{1}$为线面角，$\theta$为射影角，如图②，我们给出如下三角形，
　　
在图②中，$\triangle OAB$，$\triangle OBC$，$\triangle ABC$是直角三角形，则$\cos\beta = \frac{BC}{AB}$，$\cos\alpha_{1} = \frac{BO}{AB}$，$\cos\theta = \frac{BC}{BO}$，得到$\cos\beta = \cos\alpha_{1} · \cos\theta$，即三余弦定理得证，如图③，

作$BH \perp AA_{1}$于点$H$，作$HM \perp CC_{1}$于点$M$，连接$BM$，因为$AA_{1} // CC_{1}$，所以$HM \perp AA_{1}$，而$BH \cap HM = H$，$BH$，$HM \subset$平面$BHM$，则$AA_{1} \perp$平面$BHM$，故三棱柱$ABC - A_{1}B_{1}C_{1}$内切球半径等于$\triangle BHM$的内切圆半径，在$BH = 8\sin\angle A_{1}AB = 8 × \frac{\sqrt{3}}{4} = 2\sqrt{3}$，而平面$AA_{1}B_{1}B \perp$平面$ABC$，由三余弦定理得$\cos\angle A_{1}AC = \cos\angle A_{1}AB · \cos\angle BAC = \frac{\sqrt{13}}{4} × \frac{4}{5} = \frac{\sqrt{13}}{5}$，结合三角函数的基本关系得$\sin\angle A_{1}AC = \frac{\sqrt{12}}{5}$，故$HM = AC · \sin\angle A_{1}AC = 5 × \frac{\sqrt{12}}{5} = 2\sqrt{3}$，同理$\cos\angle B_{1}BC = \cos\angle B_{1}BA · \cos\angle ABC = - \frac{\sqrt{13}}{5}$，得到$BM = BC · \sin\angle BCC_{1} = 5\sin\angle B_{1}BC = 2\sqrt{3}$.因为$\cos\angle A_{1}AB = \frac{\sqrt{13}}{4}$，所以$\frac{BH}{\sin\angle A_{1}AB} = \frac{\sqrt{3}}{8} = \frac{\sqrt{3}}{4}$，解得$BH = 2\sqrt{3}$，则$HM = BM = BH = 2\sqrt{3}$，则$\triangle BHM$为正三角形，设内接球半径为$r$，则$S_{\triangle BHM} = \frac{1}{2}(BM + BH + HM)r = \frac{\sqrt{3}}{4}BM^{2}$，解得$r = 1$.因为$AB = 8$，$AC = BC = 5$，所以由余弦定理得$\cos\angle ACB = \frac{5^{2} + 5^{2} - 8^{2}}{2 × 5 × 5} = - \frac{7}{25}$，且$\sin\angle ACB ＞ 0$，由同角三角函数的性质得$\sin\angle ACB = \frac{24}{25}$，所以$S_{\triangle ABC} = \frac{1}{2} × 5 × 5 × \frac{24}{25} = 12$，因为$r = 1$，所以三棱柱的高为$2r = 2$，则$V_{ABC - A_{1}B_{1}C_{1}} = 12 × 2 = 24$.