《2025年学霸高考黑题数学人教版》

变式训练1. (2025·河南三门峡模拟)图①是边长为1的正六边形ABCDEF，将其沿直线FC折叠成如图②的空间图形A'E'F'-B'D'C'，若A'E' = $\frac{3}{2}$，则几何体A'E'F'-B'D'C'的体积为 (D)


A.$\frac{3\sqrt{3}}{8}$
B.$\frac{5\sqrt{3}}{16}$
C.$\frac{3\sqrt{3}}{16}$
D.$\frac{\sqrt{3}}{4}$

答案：
变式训练1.D解析：过$A'$作$A'G\perp C'F'$，垂足为$G$，连接$E'G$，由对称性可得$E'G\perp C'F'$，又$A'G\cap E'G = G$，$A'G$，$E'G\subset$平面$A'GE'$，$C'F'\perp$平面$A'GE'$，过$B'$作$B'H\perp C'F'$，垂足为$H$，连接$D'H$，则$D'H\perp C'F'$，所以$A'G// B'H$，又$A'G\not\subset$平面$B'HD'$，$B'H\subset$平面$B'HD'$，$D'H\subset$平面$B'HD'$，所以$E'G//$平面$B'HD'$，又$A'G\cap E'G = G$，$A'G$，$E'G\subset$平面$A'GE'$，所以平面$A'GE'//$平面$B'HD'$，即空间几何体$A'GE'-B'HD'$为直三棱柱.因为$A'F' = 1$，$\angle A'F'G = 60°$，所以$A'G=\frac{\sqrt{3}}{2}$，$F'G=\frac{1}{2}$，同理求得$E'G=\frac{\sqrt{3}}{2}$，$C'H=\frac{1}{2}$，则$GH = 1$，又$A'E'=\frac{3}{2}$，等腰三角形$A'GE'$的面积为$S=\frac{1}{2}×\frac{3}{2}×\sqrt{\left(\frac{\sqrt{3}}{2}\right)^2-\left(\frac{3}{4}\right)^2}=\frac{3\sqrt{3}}{16}$，空间几何体$A'E'F'-B'D'C'$拆分为三棱柱$A'GE'-B'HD'$、三棱锥$F'-A'GE'$和三棱锥$C'-B'HD'$三个部分，所以空间几何体$A'E'F'-B'D'C'$的体积为$V=\frac{3\sqrt{3}}{16}×1 + 2×\frac{1}{3}×\frac{3\sqrt{3}}{16}×\frac{1}{2}=\frac{\sqrt{3}}{4}$.

变式训练2. (多选)(2025·河北石家庄模拟)如图①，在矩形ABCD中，AB = 1，BC = $\sqrt{3}$，点M为线段BC上的动点(含C点，不含B点)，将△ABM沿AM折起，使点B翻折至B'位置，如图②，且二面角B'-AM-D为60°，点N为线段B'D上的动点，在四棱锥B'-AMCD中，下列说法错误的是 (BCD)


A.存在点N使得CN//平面B'AM
B.存在点M使得对于任意点N都有直线B'M和直线CN垂直
C.三棱锥B'-AMC的体积为定值
D.二面角B'-CM-D的正切值的最小值为$\frac{2}{3}$

答案：
变式训练2.BCD解析：如图①，在线段$AD$上截取$AE = CM$，由$AD// CM$，可得四边形$AMCE$为平行四边形，则$CE// AM$，又$CE\not\subset$平面$AMB'$，$AM\subset$平面$AMB'$，则$CE//$平面$AMB'$.在平面$AB'D$内过点$E$作$EN// AB'$，$EN\not\subset$平面$AMB'$，$AB'\subset$平面$AMB'$，则$EN//$平面$AMB'$，又$EN\cap CE = E$，则平面$CEN//$平面$B'AM$，又$CN\subset$平面$CEN$，$\therefore CN//$平面$B'AM$，故A正确.

若对于任意点$N$都有直线$B'M$和直线$CN$垂直，$CN\subset$平面$B'CD$，则$B'M\perp$平面$B'CD$，又$B'D\subset$平面$B'CD$，$\therefore B'M\perp B'D$，又$B'M\perp AB'$，且$B'D\cap B'A = B'$，$B'D$，$B'A\subset$平面$AB'D$，$\therefore B'M\perp$平面$AB'D$，显然$B'M$不可能同时垂直于两个相交平面，故B错误.如图②，过$B'$作$B'O\perp$平面$AMCD$于点$O$，过$O$作$OP\perp AM$于点$P$，连接$B'P$，由$B'O\perp$平面$AMCD$，$AM\subset$平面$AMCD$，则$B'O\perp AM$，又$OP\cap B'O = O$，$OP$，$B'O\subset$平面$OPB'$，则$AM\perp$平面$OPB'$，又$B'P\subset$平面$OPB'$，则$B'P\perp AM$，$\therefore\angle B'PO$为二面角$B'-AM - D$的平面角，$\therefore\angle B'PO = 60°$.

设$B'M = t$，则$MC=\sqrt{3}-t$，当$t=\sqrt{3}$时，$M$，$C$重合，不合题意，则$t\in(0,\sqrt{3})$.在$Rt\triangle AB'M$中，由等面积法可知$B'P=\frac{t}{\sqrt{1 + t^2}}$，$\therefore B'O=\frac{\sqrt{3}t}{2\sqrt{1 + t^2}}$，$\therefore V_{B'-AMC}=\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{3}t}{2\sqrt{1 + t^2}}× t=\frac{\sqrt{3}t^2}{12(1 + t^2)}$，设二面角$B'-CM - D$的大小为$\theta$，则$\tan\theta=\frac{B'O}{OQ}=\frac{\frac{\sqrt{3}t}{2\sqrt{1 + t^2}}}{\frac{t^2}{1 + t^2}}=\frac{\sqrt{3}}{2}×\frac{1 + t^2}{t}$，设$\frac{1}{t}=\frac{\sqrt{3}}{2}×\sqrt{1 + t^2}$，当$t=\sqrt{3}$时，$\tan\theta$取最小值$\frac{2}{3}$，$\because t\in(0,\sqrt{3})$，$\therefore$二面角$B'-CM - D$的正切值的最小值不可能取到$\frac{2}{3}$，故D错误.

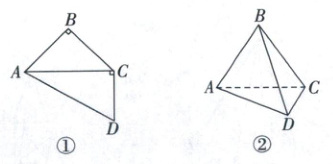
变式训练3. (多选)(2025·黑龙江佳木斯模拟)如图①所示，在四边形ABCD中，∠ABC = ∠ACD = $\frac{\pi}{2}$，∠CAD = $\frac{\pi}{6}$，AB = BC = 2$\sqrt{6}$.如图②所示，把△ABC沿AC边折起，使点B不在平面ACD内，连接BD.则下列选项正确的是 (ABD)


A.当平面ABC⊥平面ACD时，点C到平面ABD的距离为$\frac{4\sqrt{15}}{5}$
B.异面直线AB与CD所成角的取值范围为$(\frac{\pi}{4},\frac{\pi}{2}]$
C.M，N分别为CD，BC的中点，在翻转的过程中，存在某个位置，使得MN = $\sqrt{30}$
D.三棱锥B-ACD的外接球的表面积的最小值为64π

答案：
变式训练3.ABD解析：找$AC$中点$O$，作$OT// CD$，$OG\perp$平面$ACD$.因为$\angle ACD=\frac{\pi}{2}$，$OT// CD$，所以$AC\perp OT$，如图①，以$O$为原点建立空间直角坐标系.

因为$\angle ABC=\frac{\pi}{2}$，$AB = BC = 2\sqrt{6}$，所以由勾股定理得$AC = 4\sqrt{3}$.又因$\angle CAD=\frac{\pi}{6}$，则$\frac{CD}{AC}=\frac{\sqrt{3}}{3}$，解得$CD = 4$，故$O(0,0,0)$，$A(2\sqrt{3},0,0)$，$C(-2\sqrt{3},0,0)$，$D(-2\sqrt{3},4,0)$，设$B(x,y,z)(z＞0)$，则$\overrightarrow{OB}=(x,y,z)$，$\overrightarrow{AC}=(-4\sqrt{3},0,0)$，因为$OB\perp AC$，故$-4\sqrt{3}x = 0$，得$x = 0$，则$\overrightarrow{AB}=(-2\sqrt{3},y,z)$，$\overrightarrow{CB}=(2\sqrt{3},y,z)$，由$AB\perp CB$可得$y^2 + z^2 - 12 = 0$，化简得$y^2 + z^2 = 12$，即点$B$的轨迹方程是半径为$2\sqrt{3}$的圆的一部分，故$B(0,2\sqrt{3}\cos\theta,2\sqrt{3}\sin\theta)$，$\theta\in(0,\pi)$，则$\overrightarrow{AB}=(-2\sqrt{3},2\sqrt{3}\cos\theta,2\sqrt{3}\sin\theta)$.设平面$ABC$的法向量为$\mathbf{n}=(x_1,y_1,z_1)$，则$\overrightarrow{AC}·\mathbf{n}=-4\sqrt{3}x_1 = 0$，解得$x_1 = 0$，且$\overrightarrow{AB}·\mathbf{n}=2\sqrt{3}y_1\cos\theta+2\sqrt{3}z_1\sin\theta = 0$，令$y_1=\sin\theta$，解得$z_1=-\cos\theta$，得到$\mathbf{n}=(0,\sin\theta,-\cos\theta)$.易得平面$ACD$的法向量为$\mathbf{m}=(0,0,1)$.
对于$A$，当平面$ABC\perp$平面$ACD$时，$\mathbf{m}·\mathbf{n}=0$，此时$-\cos\theta = 0$，解得$\theta=\frac{\pi}{2}$，此时$B(0,2\sqrt{3})$，而$\overrightarrow{AB}=(-2\sqrt{3},0,2\sqrt{3})$，$\overrightarrow{AD}=(-4\sqrt{3},4,0)$，设平面$ABD$的法向量为$\mathbf{s}=(a,b,c)$，则$\overrightarrow{AD}·\mathbf{s}=-4\sqrt{3}a + 4b = 0$，$\overrightarrow{AB}·\mathbf{s}=-2\sqrt{3}a+2\sqrt{3}c = 0$，令$a = 1$，解得$c = 1$，$b=\sqrt{3}$，故$\mathbf{s}=(1,\sqrt{3},1)$，而$\overrightarrow{AC}=(-4\sqrt{3},0,0)$，设点$C$到平面$ABD$的距离为$d$，则$d=\frac{|\overrightarrow{AC}·\mathbf{s}|}{|\mathbf{s}|}=\frac{| - 4\sqrt{3}|}{\sqrt{1 + 1 + (\sqrt{3})^2}}=\frac{4\sqrt{15}}{5}$，故A正确.对于$B$，由已知得$\overrightarrow{CD}=(0,4,0)$，$\overrightarrow{AB}=(-2\sqrt{3},2\sqrt{3}\cos\theta,2\sqrt{3}\sin\theta)$，设异面直线$AB$与$CD$所成角为$\beta$，且$\beta\in\left(0,\frac{\pi}{2}\right]$，则$\cos\beta=\frac{|\overrightarrow{AB}·\overrightarrow{DC}|}{|\overrightarrow{AB}|·|\overrightarrow{DC}|}=\frac{18\sqrt{3}\cos\theta}{4×\sqrt{(-2\sqrt{3})^2+(2\sqrt{3}\cos\theta)^2+(2\sqrt{3}\sin\theta)^2}}$，结合余弦函数性质得$|\cos\theta|\in[0,1)$，故$\cos\beta\in\left[0,\frac{\sqrt{2}}{2}\right]$，由余弦函数性质解得$\beta\in\left[\frac{\pi}{4},\frac{\pi}{2}\right]$，故B正确.对于$C$，因为$M$，$N$分别为$CD$，$BC$的中点，如图②，所以$M(-2\sqrt{3},2,0)$，$N(-\sqrt{3},\sqrt{3}\cos\theta,\sqrt{3}\sin\theta)$，则$MN=\sqrt{3+(2-\sqrt{3}\cos\theta)^2}$，令$MN=\sqrt{30}$，则$\sqrt{3+(2-\sqrt{3}\cos\theta)^2}=\sqrt{30}$，无解，所以在翻折的过程中，不存在某个位置，使得$MN=\sqrt{30}$，故C错误.
对于$D$，首先，我们来证明求解外接球半径的一个模型，我们给定三棱锥$P - ABC$，设$O_1$，$O_2$分别是$\triangle ABP$，$\triangle ABC$的外心，设外接球球心为$O$，$M$是$AB$中点，则$O_1M\perp AB$，$O_2M\perp AB$，所以$\angle O_1MO_2$是二面角$P - AB - C$的平面角，设$\angle O_1MO_2=\alpha$，设$O_1M = m$，$O_2M = n$，$O_1O_2=l$，连接$O_1O$，$O_2O$，则$O_1O\perp$平面$PAB$，$OO_2\perp$平面$ABC$，

在四边形$OO_1MO_2$中，可得$\angle OO_1M=\angle OO_2M=\frac{\pi}{2}$，所以$O$，$O_1$，$M$，$O_2$四点共圆，且设四边形$OO_1MO_2$的外接圆半径为$r$，所以$OM = 2r$，连接$O_1O_2$，$OM$，由正弦定理得$\frac{O_1O_2}{\sin\alpha}=2r$，设$O_1O_2=c$，故$OM=\frac{c}{\sin\alpha}$，而在$\triangle MO_1O_2$中，由余弦定理得$c^2=m^2 + n^2-2mn\cos\alpha$，连接$OA$，$OB$，所以$OA = OB$，则得$OM\perp AB$，且$BM=\frac{l}{2}$，设$OA = OB = R$，在直角三角形$OBM$中，$R^2=\frac{c^2}{\sin^2\alpha}+\frac{l^2}{4}$，所以$R^2=\frac{m^2 + n^2-2mn\cos\alpha}{\sin^2\alpha}+\frac{l^2}{4}$，即该模型得证.设二面角$B - AC - D$的大小为$\alpha$，且$\alpha\in[0,\pi]$，$AC = l = 4\sqrt{3}$，如图④，$\triangle ABC$的外心为$O$，找$AD$中点$Q$作为$\triangle ACD$外心，

则由中位线性质得$OQ = 2$，得到$m = 0$，$n = 2$，此时公式变为$R^2=\frac{4}{\sin^2\alpha}+\frac{(4\sqrt{3})^2}{4}=\frac{4}{\sin^2\alpha}+12$，若三棱锥$B - ACD$的外接球的表面积最小，则其半径一定最小，由上述分析可得$R^2=\frac{4}{\sin^2\alpha}+12$，而$\alpha\in[0,\pi]$，结合正弦函数性质可得当$\sin^2\alpha = 1$时$R^2$最小，即$R^2 = 4 + 12 = 16$，由球的表面积公式得表面积为$4\pi×16 = 64\pi$，则三棱锥$B - ACD$的外接球的表面积的最小值为$64\pi$，故D正确.