2025年学霸高考黑题化学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学霸高考黑题化学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
经典真题 1 (2025·湖北,14,3 分)
铜(I)、乙腈(简写为 L)的某水溶液体系中含铜物种的分布曲线如图。纵坐标(δ)为含铜物种占总铜的物质的量分数,总铜浓度为 1.0×10⁻³ mol·L⁻¹。下列描述正确的是(

A.Cu⁺ + 3L ⇌ [CuL₃]⁺的 lgK = 0.27
B.当 c(Cu⁺) = c{[CuL]⁺}时,c{[CuL₂]⁺} = 2.0×10⁻⁴ mol·L⁻¹
C.n 从 0 增加到 2,[CuLₙ]⁺结合 L 的能力随减小
D.若 c{[CuL]⁺} = c{[CuL₃]⁺},则 2c{[CuL₂]⁺} < c{[CuL]⁺} + 3c{[CuL₃]⁺}
铜(I)、乙腈(简写为 L)的某水溶液体系中含铜物种的分布曲线如图。纵坐标(δ)为含铜物种占总铜的物质的量分数,总铜浓度为 1.0×10⁻³ mol·L⁻¹。下列描述正确的是(
C
)
A.Cu⁺ + 3L ⇌ [CuL₃]⁺的 lgK = 0.27
B.当 c(Cu⁺) = c{[CuL]⁺}时,c{[CuL₂]⁺} = 2.0×10⁻⁴ mol·L⁻¹
C.n 从 0 增加到 2,[CuLₙ]⁺结合 L 的能力随减小
D.若 c{[CuL]⁺} = c{[CuL₃]⁺},则 2c{[CuL₂]⁺} < c{[CuL]⁺} + 3c{[CuL₃]⁺}
答案:
经典真题1C
解题思路
物质分布曲线题目常通过交点来计算化学平衡常数$K$。在判断溶液中离子浓度大小时要灵活运用溶液中的电荷守恒、物料守恒、质子守恒。
解析:$\mathrm{Cu^{+} + 3L \rightleftharpoons [CuL_3]^+}$的$K = \frac{c[ \mathrm{[CuL_3]^+} ]}{c(\mathrm{Cu^+}) × c^3(\mathrm{L})}$,当图中$\delta \mathrm{[CuL_3]^+} = \delta \mathrm{Cu^+}$时,$K = \frac{1}{c^3(\mathrm{L})}$,$\lg K = -3 \lg c(\mathrm{L})$,由图像可知,此时$-1.6 < \lg c(\mathrm{L}) < -1.2$,则$\lg K \neq 0.27$,A错误;当$c(\mathrm{Cu^+}) = c \mathrm{[CuL_3]^+}$时,由图像可知,$\delta \mathrm{Cu^+} = \delta \mathrm{[CuL_3]^+} = 0.48$,$\delta \mathrm{[CuL_3]^+}$可忽略不计,则$\delta \mathrm{[CuL_2]^+} = 0.04$,$c \mathrm{[CuL_2]^+} = 0.04 × 1.0 × 10^{-3} \mathrm{mol · L^{-1}} = 4 × 10^{-5} \mathrm{mol · L^{-1}}$,B错误;$\mathrm{[CuL_n]^+}$结合L的离子方程式为$\mathrm{[CuL_n]^+ + L \rightleftharpoons [CuL_{n+1}]^+}$,当$\delta \mathrm{[CuL_n]^+} = \delta \mathrm{[CuL_{n+1}]^+}$时,$K = \frac{1}{c(\mathrm{L})}$,由图像交点可知,随着$n$变大,$c(\mathrm{L})$逐渐变大,则$K$值变小,说明$\mathrm{[CuL_n]^+}$结合L的能力随之减小,C正确;若$c \mathrm{[CuL_3]^+} = c \mathrm{[CuL_3]^+}$,由图像交点可知,$\delta \mathrm{[CuL_3]^+} = \delta \mathrm{[CuL_3]^+} < 0.3$,$\delta \mathrm{[CuL_2]^+} > 0.6$,则$2c \mathrm{[CuL_2]^+} > c \mathrm{[CuL_3]^+} + 3c \mathrm{[CuL_3]^+}$,D错误。
解题思路
物质分布曲线题目常通过交点来计算化学平衡常数$K$。在判断溶液中离子浓度大小时要灵活运用溶液中的电荷守恒、物料守恒、质子守恒。
解析:$\mathrm{Cu^{+} + 3L \rightleftharpoons [CuL_3]^+}$的$K = \frac{c[ \mathrm{[CuL_3]^+} ]}{c(\mathrm{Cu^+}) × c^3(\mathrm{L})}$,当图中$\delta \mathrm{[CuL_3]^+} = \delta \mathrm{Cu^+}$时,$K = \frac{1}{c^3(\mathrm{L})}$,$\lg K = -3 \lg c(\mathrm{L})$,由图像可知,此时$-1.6 < \lg c(\mathrm{L}) < -1.2$,则$\lg K \neq 0.27$,A错误;当$c(\mathrm{Cu^+}) = c \mathrm{[CuL_3]^+}$时,由图像可知,$\delta \mathrm{Cu^+} = \delta \mathrm{[CuL_3]^+} = 0.48$,$\delta \mathrm{[CuL_3]^+}$可忽略不计,则$\delta \mathrm{[CuL_2]^+} = 0.04$,$c \mathrm{[CuL_2]^+} = 0.04 × 1.0 × 10^{-3} \mathrm{mol · L^{-1}} = 4 × 10^{-5} \mathrm{mol · L^{-1}}$,B错误;$\mathrm{[CuL_n]^+}$结合L的离子方程式为$\mathrm{[CuL_n]^+ + L \rightleftharpoons [CuL_{n+1}]^+}$,当$\delta \mathrm{[CuL_n]^+} = \delta \mathrm{[CuL_{n+1}]^+}$时,$K = \frac{1}{c(\mathrm{L})}$,由图像交点可知,随着$n$变大,$c(\mathrm{L})$逐渐变大,则$K$值变小,说明$\mathrm{[CuL_n]^+}$结合L的能力随之减小,C正确;若$c \mathrm{[CuL_3]^+} = c \mathrm{[CuL_3]^+}$,由图像交点可知,$\delta \mathrm{[CuL_3]^+} = \delta \mathrm{[CuL_3]^+} < 0.3$,$\delta \mathrm{[CuL_2]^+} > 0.6$,则$2c \mathrm{[CuL_2]^+} > c \mathrm{[CuL_3]^+} + 3c \mathrm{[CuL_3]^+}$,D错误。
经典真题 2 (2025·黑吉辽蒙,15,3 分)
室温下将 0.1 mol AgCl 置于 0.1 mol·L⁻¹ NH₄NO₃溶液中,保持溶液体积和 N 元素总物质的量不变,pX-pH 曲线如图,Ag⁺ + NH₃ ⇌ [Ag(NH₃)]⁺和 Ag⁺ + 2NH₃ ⇌ [Ag(NH₃)₂]⁺的平衡常数分别为 K₁ 和 K₂;NH₄⁺的水解常数 Kₕ(NH₄⁺) = 10⁻⁹.²⁵。下列说法错误的是(
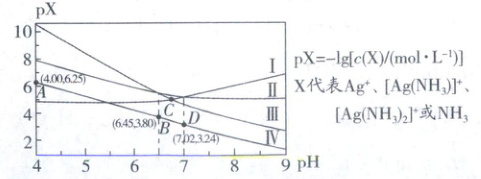
A.Ⅲ为[Ag(NH₃)₂]⁺的变化曲线
B.D 点:c(NH₄⁺) - c(OH⁻) > 0.1 - c(H⁺)
C.K₁ = 10³.²⁴
D.C 点:c(NH₃) = 10⁻³.⁵² mol·L⁻¹
室温下将 0.1 mol AgCl 置于 0.1 mol·L⁻¹ NH₄NO₃溶液中,保持溶液体积和 N 元素总物质的量不变,pX-pH 曲线如图,Ag⁺ + NH₃ ⇌ [Ag(NH₃)]⁺和 Ag⁺ + 2NH₃ ⇌ [Ag(NH₃)₂]⁺的平衡常数分别为 K₁ 和 K₂;NH₄⁺的水解常数 Kₕ(NH₄⁺) = 10⁻⁹.²⁵。下列说法错误的是(
B
)
A.Ⅲ为[Ag(NH₃)₂]⁺的变化曲线
B.D 点:c(NH₄⁺) - c(OH⁻) > 0.1 - c(H⁺)
C.K₁ = 10³.²⁴
D.C 点:c(NH₃) = 10⁻³.⁵² mol·L⁻¹
答案:
经典真题2B
解题思路
本题中pH越小,酸性越强,$\mathrm{Ag^+}$浓度越大,氨气浓度越小,所以Ⅲ代表$\mathrm{[Ag(NH_3)_2]^+}$,Ⅱ代表$\mathrm{[Ag(NH_3)]^+}$,Ⅳ代表$\mathrm{NH_3}$,Ⅰ代表$\mathrm{Ag^+}$。
解析:根据以上分析可知Ⅲ为$\mathrm{[Ag(NH_3)_2]^+}$的变化曲线,A正确;硝酸铵为强酸弱碱盐,其溶液$\mathrm{pH < 7}$,图像pH增大至碱性,则外加了物质,又整个过程保持溶液体积和N元素总物质的量不变,则所加物质不是氨水,若不外加物质,则溶液中存在电荷守恒:$c(\mathrm{NH_4^+}) + c(\mathrm{[Ag(NH_3)_2]^+}) + c(\mathrm{H^+}) + c(\mathrm{Ag^+}) = c(\mathrm{OH^-}) + c(\mathrm{Cl^-}) + c(\mathrm{NO_3^-})$,物料守恒:$c(\mathrm{Ag^+}) + c(\mathrm{[Ag(NH_3)_2]^+}) + c(\mathrm{[Ag(NH_3)]^+}) = c(\mathrm{Cl^-}) = 0.1 \mathrm{mol · L^{-1}}$,$c(\mathrm{NH_4^+}) + c(\mathrm{H^+}) = 0.1 + c(\mathrm{OH^-})$,$c(\mathrm{[Ag(NH_3)_2]^+}) - c(\mathrm{OH^-}) < 0.1 - c(\mathrm{H^+})$,B错误;根据图像可知D点时$\mathrm{[Ag(NH_3)_2]^+}$和$\mathrm{Ag^+}$浓度相等,此时氨气浓度是$10^{-3.24}$,根据$\mathrm{Ag^+ + NH_3 \rightleftharpoons [Ag(NH_3)]^+}$可知$K_1 = 10^{3.24}$,C正确;C点时$\mathrm{[Ag(NH_3)_2]^+}$和$\mathrm{Ag^+}$浓度相等,B点时$\mathrm{[Ag(NH_3)_2]^+}$和$\mathrm{[Ag(NH_3)]^+}$浓度相等,所以反应$\mathrm{[Ag(NH_3)_2]^+ + NH_3 \rightleftharpoons [Ag(NH_3)_2]^+}$的平衡常数为$10^{3.8}$,因此$K_2 = 10^{3.24} × 10^{3.8} = 10^{7.04}$,C点时$\mathrm{[Ag(NH_3)_2]^+}$和$\mathrm{Ag^+}$浓度相等,因此$c(\mathrm{NH_3}) = \sqrt{10^{-7.04}} \mathrm{mol · L^{-1}} = 10^{-3.52} \mathrm{mol · L^{-1}}$,D正确。
解题思路
本题中pH越小,酸性越强,$\mathrm{Ag^+}$浓度越大,氨气浓度越小,所以Ⅲ代表$\mathrm{[Ag(NH_3)_2]^+}$,Ⅱ代表$\mathrm{[Ag(NH_3)]^+}$,Ⅳ代表$\mathrm{NH_3}$,Ⅰ代表$\mathrm{Ag^+}$。
解析:根据以上分析可知Ⅲ为$\mathrm{[Ag(NH_3)_2]^+}$的变化曲线,A正确;硝酸铵为强酸弱碱盐,其溶液$\mathrm{pH < 7}$,图像pH增大至碱性,则外加了物质,又整个过程保持溶液体积和N元素总物质的量不变,则所加物质不是氨水,若不外加物质,则溶液中存在电荷守恒:$c(\mathrm{NH_4^+}) + c(\mathrm{[Ag(NH_3)_2]^+}) + c(\mathrm{H^+}) + c(\mathrm{Ag^+}) = c(\mathrm{OH^-}) + c(\mathrm{Cl^-}) + c(\mathrm{NO_3^-})$,物料守恒:$c(\mathrm{Ag^+}) + c(\mathrm{[Ag(NH_3)_2]^+}) + c(\mathrm{[Ag(NH_3)]^+}) = c(\mathrm{Cl^-}) = 0.1 \mathrm{mol · L^{-1}}$,$c(\mathrm{NH_4^+}) + c(\mathrm{H^+}) = 0.1 + c(\mathrm{OH^-})$,$c(\mathrm{[Ag(NH_3)_2]^+}) - c(\mathrm{OH^-}) < 0.1 - c(\mathrm{H^+})$,B错误;根据图像可知D点时$\mathrm{[Ag(NH_3)_2]^+}$和$\mathrm{Ag^+}$浓度相等,此时氨气浓度是$10^{-3.24}$,根据$\mathrm{Ag^+ + NH_3 \rightleftharpoons [Ag(NH_3)]^+}$可知$K_1 = 10^{3.24}$,C正确;C点时$\mathrm{[Ag(NH_3)_2]^+}$和$\mathrm{Ag^+}$浓度相等,B点时$\mathrm{[Ag(NH_3)_2]^+}$和$\mathrm{[Ag(NH_3)]^+}$浓度相等,所以反应$\mathrm{[Ag(NH_3)_2]^+ + NH_3 \rightleftharpoons [Ag(NH_3)_2]^+}$的平衡常数为$10^{3.8}$,因此$K_2 = 10^{3.24} × 10^{3.8} = 10^{7.04}$,C点时$\mathrm{[Ag(NH_3)_2]^+}$和$\mathrm{Ag^+}$浓度相等,因此$c(\mathrm{NH_3}) = \sqrt{10^{-7.04}} \mathrm{mol · L^{-1}} = 10^{-3.52} \mathrm{mol · L^{-1}}$,D正确。
经典真题 3 (2025·云南,14,3 分)
甲醛法测定 NH₄⁺的反应原理为 4NH₄⁺ + 6HCHO = (CH₂)₆N₄H⁺ + 3H⁺ + 6H₂O。取含 NH₄Cl 的废水浓缩至原体积的 1/10 后,移取 20.00 mL,加入足量甲醛反应后,用 0.010 00 mol·L⁻¹ 的 NaOH 标准溶液滴定。滴定曲线如图 1,含氮微粒的分布分数 δ 与 pH 关系如图 2{比如:δ[(CH₂)₆N₄H⁺] = c[(CH₂)₆N₄H⁺]/(c[(CH₂)₆N₄H⁺] + c[(CH₂)₆N₄])}。下列说法正确的是(
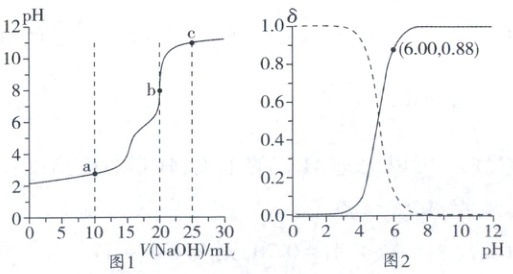
A.废水中 NH₄⁺的含量为 20.00 mg·L⁻¹
B.c 点:c[(CH₂)₆N₄H⁺] + c(H⁺) = c(OH⁻)
C.a 点:c[(CH₂)₆N₄H⁺] > c(H⁺) > c(OH⁻) > c[(CH₂)₆N₄]
D.(CH₂)₆N₄H⁺ ⇌ (CH₂)₆N₄ + H⁺的平衡常数 K ≈ 7.3×10⁻⁶
甲醛法测定 NH₄⁺的反应原理为 4NH₄⁺ + 6HCHO = (CH₂)₆N₄H⁺ + 3H⁺ + 6H₂O。取含 NH₄Cl 的废水浓缩至原体积的 1/10 后,移取 20.00 mL,加入足量甲醛反应后,用 0.010 00 mol·L⁻¹ 的 NaOH 标准溶液滴定。滴定曲线如图 1,含氮微粒的分布分数 δ 与 pH 关系如图 2{比如:δ[(CH₂)₆N₄H⁺] = c[(CH₂)₆N₄H⁺]/(c[(CH₂)₆N₄H⁺] + c[(CH₂)₆N₄])}。下列说法正确的是(
D
)
A.废水中 NH₄⁺的含量为 20.00 mg·L⁻¹
B.c 点:c[(CH₂)₆N₄H⁺] + c(H⁺) = c(OH⁻)
C.a 点:c[(CH₂)₆N₄H⁺] > c(H⁺) > c(OH⁻) > c[(CH₂)₆N₄]
D.(CH₂)₆N₄H⁺ ⇌ (CH₂)₆N₄ + H⁺的平衡常数 K ≈ 7.3×10⁻⁶
答案:
经典真题3D
解题思路
滴定曲线图常关注滴定一半时、溶液$\mathrm{pH = 7}$时、滴定终点时曲线对应的点。
解析:由图1中的信息可知,当加入$\mathrm{NaOH}$标准溶液的体积为$20.00 \mathrm{mL}$时到达滴定终点,由关系式$4\mathrm{NH_4^+} \sim \mathrm{[CH_2]_6N_4H^+} + 3\mathrm{H^+} = 4\mathrm{OH^-}$可知,由待测液的体积和标准溶液的体积相同,因此,浓缩后的$20.00 \mathrm{mL}$溶液中$c(\mathrm{NH_4^+}) = c(\mathrm{OH^-}) = 0.01000 \mathrm{mol · L^{-1}}$,则原废水中$c(\mathrm{NH_4^+}) = 0.01000 \mathrm{mol · L^{-1}} × \frac{1}{10} = 0.001000 \mathrm{mol · L^{-1}}$,因此,废水中$\mathrm{NH_4^+}$的含量为$0.001000 \mathrm{mol · L^{-1}} × 18000 \mathrm{mg · mol^{-1}} = 18.00 \mathrm{mg · L^{-1}}$,A错误;c点加入$\mathrm{NaOH}$标准溶液的体积过量,且只过量了$\frac{1}{5}$,由电荷守恒可知,$c(\mathrm{[CH_2]_6N_4H^+}) + c(\mathrm{H^+}) + c(\mathrm{Na^+}) = c(\mathrm{OH^-}) + c(\mathrm{Cl^-})$,浓缩后的废水中$\mathrm{NH_4Cl}$的浓度是$\mathrm{NaOH}$标准溶液浓度的4倍,$\mathrm{Cl^-}$和$\mathrm{Na^+}$均不参与离子反应,可以估算$c(\mathrm{Cl^-}) > c(\mathrm{Na^+})$,$c(\mathrm{[CH_2]_6N_4H^+}) + c(\mathrm{H^+}) > c(\mathrm{OH^-})$,B错误;$(\mathrm{CH_2)_6N_4H^+}$在溶液中水解使溶液显酸性,比$\mathrm{NH_3}$可知$(\mathrm{CH_2)_6N_4}$在溶液中与水作用发生电离而使溶液显碱性;a点为半滴定点,由其纵坐标可知溶液显酸性,说明$(\mathrm{CH_2)_6N_4H^+}$的水解作用强于$(\mathrm{CH_2)_6N_4}$的电离作用,可知溶液中相关粒子的浓度大小关系为$c(\mathrm{[CH_2]_6N_4}) > c(\mathrm{[CH_2]_6N_4H^+})$,C错误;由图1和图2可知,当$\mathrm{pH = 6.00}$时,$(\mathrm{CH_2)_6N_4}$占比较高,$\delta(\mathrm{[CH_2]_6N_4}) = 0.88$,则由氮原子守恒可知,$\delta(\mathrm{[CH_2]_6N_4H^+}) = 0.12$,两种粒子的浓度之比等于其分布分数之比,则$(\mathrm{CH_2)_6N_4H^+} \rightleftharpoons (\mathrm{CH_2)_6N_4} + \mathrm{H^+}$的平衡常数$K = \frac{c(\mathrm{[CH_2]_6N_4}) × c(\mathrm{H^+})}{c(\mathrm{[CH_2]_6N_4H^+})} = \frac{0.88 × 10^{-6}}{0.12} \approx 7.3 × 10^{-6}$,D正确。
解题思路
滴定曲线图常关注滴定一半时、溶液$\mathrm{pH = 7}$时、滴定终点时曲线对应的点。
解析:由图1中的信息可知,当加入$\mathrm{NaOH}$标准溶液的体积为$20.00 \mathrm{mL}$时到达滴定终点,由关系式$4\mathrm{NH_4^+} \sim \mathrm{[CH_2]_6N_4H^+} + 3\mathrm{H^+} = 4\mathrm{OH^-}$可知,由待测液的体积和标准溶液的体积相同,因此,浓缩后的$20.00 \mathrm{mL}$溶液中$c(\mathrm{NH_4^+}) = c(\mathrm{OH^-}) = 0.01000 \mathrm{mol · L^{-1}}$,则原废水中$c(\mathrm{NH_4^+}) = 0.01000 \mathrm{mol · L^{-1}} × \frac{1}{10} = 0.001000 \mathrm{mol · L^{-1}}$,因此,废水中$\mathrm{NH_4^+}$的含量为$0.001000 \mathrm{mol · L^{-1}} × 18000 \mathrm{mg · mol^{-1}} = 18.00 \mathrm{mg · L^{-1}}$,A错误;c点加入$\mathrm{NaOH}$标准溶液的体积过量,且只过量了$\frac{1}{5}$,由电荷守恒可知,$c(\mathrm{[CH_2]_6N_4H^+}) + c(\mathrm{H^+}) + c(\mathrm{Na^+}) = c(\mathrm{OH^-}) + c(\mathrm{Cl^-})$,浓缩后的废水中$\mathrm{NH_4Cl}$的浓度是$\mathrm{NaOH}$标准溶液浓度的4倍,$\mathrm{Cl^-}$和$\mathrm{Na^+}$均不参与离子反应,可以估算$c(\mathrm{Cl^-}) > c(\mathrm{Na^+})$,$c(\mathrm{[CH_2]_6N_4H^+}) + c(\mathrm{H^+}) > c(\mathrm{OH^-})$,B错误;$(\mathrm{CH_2)_6N_4H^+}$在溶液中水解使溶液显酸性,比$\mathrm{NH_3}$可知$(\mathrm{CH_2)_6N_4}$在溶液中与水作用发生电离而使溶液显碱性;a点为半滴定点,由其纵坐标可知溶液显酸性,说明$(\mathrm{CH_2)_6N_4H^+}$的水解作用强于$(\mathrm{CH_2)_6N_4}$的电离作用,可知溶液中相关粒子的浓度大小关系为$c(\mathrm{[CH_2]_6N_4}) > c(\mathrm{[CH_2]_6N_4H^+})$,C错误;由图1和图2可知,当$\mathrm{pH = 6.00}$时,$(\mathrm{CH_2)_6N_4}$占比较高,$\delta(\mathrm{[CH_2]_6N_4}) = 0.88$,则由氮原子守恒可知,$\delta(\mathrm{[CH_2]_6N_4H^+}) = 0.12$,两种粒子的浓度之比等于其分布分数之比,则$(\mathrm{CH_2)_6N_4H^+} \rightleftharpoons (\mathrm{CH_2)_6N_4} + \mathrm{H^+}$的平衡常数$K = \frac{c(\mathrm{[CH_2]_6N_4}) × c(\mathrm{H^+})}{c(\mathrm{[CH_2]_6N_4H^+})} = \frac{0.88 × 10^{-6}}{0.12} \approx 7.3 × 10^{-6}$,D正确。
查看更多完整答案,请扫码查看


