2025年学霸高考黑题化学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学霸高考黑题化学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
(2025·山东潍坊一模)$Fe^{3+}$ 可用于处理含 $I^{-}$ 废水。一定温度下,$FeCl_{3}$ 与 KI 混合溶液中存在如下反应(反应过程中忽略碘单质的挥发与阳离子的水解)。
Ⅰ.$2Fe^{3+}(aq)+2I^{-}(aq)\xlongequal{}2Fe^{2+}(aq)+I_{2}(aq)$ $\Delta H_{1}$
Ⅱ.$I_{2}(aq)+I^{-}(aq)\xlongequal{}I_{3}^{-}(aq)$ $\Delta H_{2}=akJ· mol^{-1}$
回答下列问题:

(1)反应Ⅲ:$2Fe^{3+}(aq)+3I^{-}(aq)\xlongequal{}2Fe^{2+}(aq)+I_{3}^{-}(aq)$ $\Delta H_{3}=bkJ· mol^{-1}$,则反应Ⅰ的焓变 $\Delta H_{1}=$
(2)已知:反应Ⅰ的正反应速率 $v_{正}=k_{正}· c^{m}(I^{-})· c^{n}(Fe^{3+})$ ($k_{正}$ 为正反应速率常数),改变 $I^{-}$、$Fe^{3+}$ 的浓度,反应Ⅰ的正反应速率如下表所示:
$I^{-}$ 浓度对反应速率的影响大于 $Fe^{3+}$ 浓度对反应速率的影响,理由为
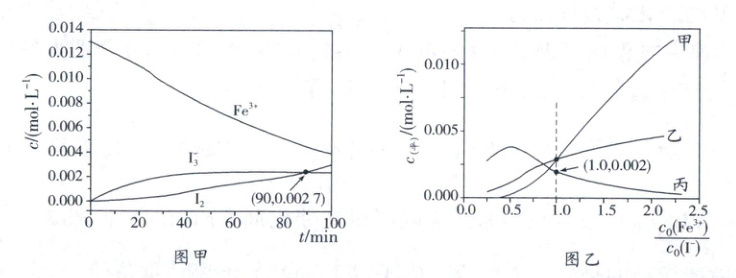
(3)保持混合溶液中 $c_{0}(FeCl_{3})+c_{0}(KI)=0.026mol· L^{-1}$,发生反应Ⅰ、Ⅱ,平衡时,$c_{平}(Fe^{3+})$、$c_{平}(I_{2})$ 与 $c_{平}(I_{3}^{-})$ 随起始投料比 $\frac{c_{0}(Fe^{3+})}{c_{0}(I^{-})}$ 的变化曲线如图乙。
①表示 $c_{平}(I_{2})$ 的曲线为
②当 $\frac{c_{0}(Fe^{3+})}{c_{0}(I^{-})}=1$ 达平衡后,溶液中 $I_{2}$ 的浓度 $c_{平}(I_{2})=$
Ⅰ.$2Fe^{3+}(aq)+2I^{-}(aq)\xlongequal{}2Fe^{2+}(aq)+I_{2}(aq)$ $\Delta H_{1}$
Ⅱ.$I_{2}(aq)+I^{-}(aq)\xlongequal{}I_{3}^{-}(aq)$ $\Delta H_{2}=akJ· mol^{-1}$
回答下列问题:

(1)反应Ⅲ:$2Fe^{3+}(aq)+3I^{-}(aq)\xlongequal{}2Fe^{2+}(aq)+I_{3}^{-}(aq)$ $\Delta H_{3}=bkJ· mol^{-1}$,则反应Ⅰ的焓变 $\Delta H_{1}=$
(b - a)
$kJ· mol^{-1}$ (用含 $a$、$b$ 的代数式表示),当 $FeCl_{3}$ 和 KI 的初始浓度均为 $0.013mol· L^{-1}$ 时,部分微粒的物质的量浓度随时间变化曲线如图甲所示。$0\sim90min$ 内,$Fe^{3+}$ 的反应速率 $v(Fe^{3+})=$$1.2×10^{-4}$
$mol· L^{-1}· min^{-1}$。(2)已知:反应Ⅰ的正反应速率 $v_{正}=k_{正}· c^{m}(I^{-})· c^{n}(Fe^{3+})$ ($k_{正}$ 为正反应速率常数),改变 $I^{-}$、$Fe^{3+}$ 的浓度,反应Ⅰ的正反应速率如下表所示:
$I^{-}$ 浓度对反应速率的影响大于 $Fe^{3+}$ 浓度对反应速率的影响,理由为
计算得m = 2,n = 1,m>n,故I⁻浓度对反应速率的影响大于Fe³⁺浓度对反应速率的影响
。(3)保持混合溶液中 $c_{0}(FeCl_{3})+c_{0}(KI)=0.026mol· L^{-1}$,发生反应Ⅰ、Ⅱ,平衡时,$c_{平}(Fe^{3+})$、$c_{平}(I_{2})$ 与 $c_{平}(I_{3}^{-})$ 随起始投料比 $\frac{c_{0}(Fe^{3+})}{c_{0}(I^{-})}$ 的变化曲线如图乙。
①表示 $c_{平}(I_{2})$ 的曲线为
乙
。②当 $\frac{c_{0}(Fe^{3+})}{c_{0}(I^{-})}=1$ 达平衡后,溶液中 $I_{2}$ 的浓度 $c_{平}(I_{2})=$
0.003
$mol· L^{-1}$,反应Ⅰ的平衡常数 $K=$$3.3×10^{4}$
$$;反应平衡后再加入少量 $CCl_{4}$ 充分振荡,重新平衡后水溶液中 $c_{平}(I_{2})· c_{平}(I^{-})$ 的值 变小
(填“变大”“变小”或“不变”)。
答案:
巩固训练3
(1)(b - a) $1.2×10^{-4}$
(2)计算得m = 2,n = 1,m>n,故I⁻浓度对反应速率的影响大于Fe³⁺浓度对反应速率的影响
(3)①乙 ②0.003 $3.3×10^{4}$ 变小
解析:
(1)由盖斯定律可知,反应Ⅲ - 反应Ⅱ可得$2Fe^{3+}(aq)+2I^{-}(aq)\rightleftharpoons2Fe^{2+}(aq)+I_{2}(aq)$ $\Delta H_{1}=\Delta H_{3}-\Delta H_{2}=(b - a)kJ·mol^{-1}$,FeCl₃和KI的初始浓度均为$0.013mol·L^{-1}$,90 min时,溶液中$c(I_{3}^{-})=c(I_{2})=0.0027mol·L^{-1}$,根据已知条件列出“三段式”:
$2Fe^{3+}(aq)+2I^{-}(aq)\rightleftharpoons2Fe^{2+}(aq)+I_{2}(aq)$
起始$(mol·L^{-1})$ 0.013 0.013 0 0
转化$(mol·L^{-1})$ 2x 2x 2x x
90 min$(mol·L^{-1})$ 0.013 - 2x 0.013 - 2x 2x x
$I_{2}(aq)+I^{-}(aq)\rightleftharpoons I_{3}^{-}(aq)$
起始$(mol·L^{-1})$ x 0.013 - 2x 0
转化$(mol·L^{-1})$ y y y
90 min$(mol·L^{-1})$ x - y 0.013 - 2x - y y
$y = 0.0027$,$x - y = 0.0027$,则$x = 0.0054$,0~90 min内,$v(Fe^{2+})=\frac{2×0.0054mol·L^{-1}}{90min}=1.2×10^{-4}mol·L^{-1}·min^{-1}$。
(2)由已知数据可知,$0.032k_{正}=k_{正}(0.20)^{m}(0.80)^{n}$,$0.128k_{正}=k_{正}(0.80)^{m}(0.20)^{n}$,$0.144k_{正}=k_{正}(0.60)^{m}(0.40)^{n}$,解得m = 2,n = 1,I⁻浓度对反应速率的影响大于Fe³⁺浓度对反应速率的影响,故理由是计算得m = 2,n = 1,m>n,故I⁻浓度对反应速率的影响大于Fe³⁺浓度对反应速率的影响。
(3)投料比$\frac{c_{0}(Fe^{3+})}{c_{0}(I^{-})}$增大;相当于减小c(I⁻),反应ⅰ平衡逆向移动,$c_{平}(Fe^{3+})$增大,反应ⅱ平衡逆向移动,$c_{平}(I_{3}^{-})$减小,$c_{平}(I_{2})$增大,$c_{平}(I_{3}^{-})$增大程度小于$c_{平}(Fe^{3+})$,则表示$c_{平}(Fe^{3+})$的是甲,表示$c_{平}(I_{2})$的曲线为乙,表示$c_{平}(I_{3}^{-})$的是丙;当$\frac{c_{0}(Fe^{3+})}{c_{0}(I^{-})}=1$达平衡后,根据已知条件列出三段式:
$2Fe^{3+}(aq)+2I^{-}(aq)\rightleftharpoons2Fe^{2+}(aq)+I_{2}(aq)$
起始$(mol·L^{-1})$ 0.013 0.013 0 0
转化$(mol·L^{-1})$ 2x 2x 2x x
90 min$(mol·L^{-1})$ 0.013 - 2x 0.013 - 2x 2x x
$I_{2}(aq)+I^{-}(aq)\rightleftharpoons I_{3}^{-}(aq)$
起始$(mol·L^{-1})$ x 0.013 - 2x 0
转化$(mol·L^{-1})$ y y y
90 min$(mol·L^{-1})$ x - y 0.013 - 2x - y y
$c_{平}(I_{3}^{-}) = y = 0.002mol·L^{-1}$,$c_{平}(Fe^{3+}) = c_{平}(I_{2}) = 0.013 - 2x = x - y$,解得$x = 0.005$,溶液中I⁻的浓度$c_{平}(I^{-}) = 0.005mol·L^{-1}-0.002mol·L^{-1}=0.003mol·L^{-1}$,反应Ⅰ的平衡常数$K=\frac{(0.005 - 0.002)×0.01^{2}}{(0.013 - 0.01)^{2}×(0.013 - 0.01)^{2}}≈3.3×10^{4}$;反应平衡后再加入少量CCl₄充分振荡,I₂进入CCl₄中,反应Ⅱ逆向移动,$c_{平}(I_{2})$减小,$c_{平}(I^{-})$增大,重新平衡后水溶液中$c_{平}(I_{2})·c_{平}(I^{-})$的值变小。
(1)(b - a) $1.2×10^{-4}$
(2)计算得m = 2,n = 1,m>n,故I⁻浓度对反应速率的影响大于Fe³⁺浓度对反应速率的影响
(3)①乙 ②0.003 $3.3×10^{4}$ 变小
解析:
(1)由盖斯定律可知,反应Ⅲ - 反应Ⅱ可得$2Fe^{3+}(aq)+2I^{-}(aq)\rightleftharpoons2Fe^{2+}(aq)+I_{2}(aq)$ $\Delta H_{1}=\Delta H_{3}-\Delta H_{2}=(b - a)kJ·mol^{-1}$,FeCl₃和KI的初始浓度均为$0.013mol·L^{-1}$,90 min时,溶液中$c(I_{3}^{-})=c(I_{2})=0.0027mol·L^{-1}$,根据已知条件列出“三段式”:
$2Fe^{3+}(aq)+2I^{-}(aq)\rightleftharpoons2Fe^{2+}(aq)+I_{2}(aq)$
起始$(mol·L^{-1})$ 0.013 0.013 0 0
转化$(mol·L^{-1})$ 2x 2x 2x x
90 min$(mol·L^{-1})$ 0.013 - 2x 0.013 - 2x 2x x
$I_{2}(aq)+I^{-}(aq)\rightleftharpoons I_{3}^{-}(aq)$
起始$(mol·L^{-1})$ x 0.013 - 2x 0
转化$(mol·L^{-1})$ y y y
90 min$(mol·L^{-1})$ x - y 0.013 - 2x - y y
$y = 0.0027$,$x - y = 0.0027$,则$x = 0.0054$,0~90 min内,$v(Fe^{2+})=\frac{2×0.0054mol·L^{-1}}{90min}=1.2×10^{-4}mol·L^{-1}·min^{-1}$。
(2)由已知数据可知,$0.032k_{正}=k_{正}(0.20)^{m}(0.80)^{n}$,$0.128k_{正}=k_{正}(0.80)^{m}(0.20)^{n}$,$0.144k_{正}=k_{正}(0.60)^{m}(0.40)^{n}$,解得m = 2,n = 1,I⁻浓度对反应速率的影响大于Fe³⁺浓度对反应速率的影响,故理由是计算得m = 2,n = 1,m>n,故I⁻浓度对反应速率的影响大于Fe³⁺浓度对反应速率的影响。
(3)投料比$\frac{c_{0}(Fe^{3+})}{c_{0}(I^{-})}$增大;相当于减小c(I⁻),反应ⅰ平衡逆向移动,$c_{平}(Fe^{3+})$增大,反应ⅱ平衡逆向移动,$c_{平}(I_{3}^{-})$减小,$c_{平}(I_{2})$增大,$c_{平}(I_{3}^{-})$增大程度小于$c_{平}(Fe^{3+})$,则表示$c_{平}(Fe^{3+})$的是甲,表示$c_{平}(I_{2})$的曲线为乙,表示$c_{平}(I_{3}^{-})$的是丙;当$\frac{c_{0}(Fe^{3+})}{c_{0}(I^{-})}=1$达平衡后,根据已知条件列出三段式:
$2Fe^{3+}(aq)+2I^{-}(aq)\rightleftharpoons2Fe^{2+}(aq)+I_{2}(aq)$
起始$(mol·L^{-1})$ 0.013 0.013 0 0
转化$(mol·L^{-1})$ 2x 2x 2x x
90 min$(mol·L^{-1})$ 0.013 - 2x 0.013 - 2x 2x x
$I_{2}(aq)+I^{-}(aq)\rightleftharpoons I_{3}^{-}(aq)$
起始$(mol·L^{-1})$ x 0.013 - 2x 0
转化$(mol·L^{-1})$ y y y
90 min$(mol·L^{-1})$ x - y 0.013 - 2x - y y
$c_{平}(I_{3}^{-}) = y = 0.002mol·L^{-1}$,$c_{平}(Fe^{3+}) = c_{平}(I_{2}) = 0.013 - 2x = x - y$,解得$x = 0.005$,溶液中I⁻的浓度$c_{平}(I^{-}) = 0.005mol·L^{-1}-0.002mol·L^{-1}=0.003mol·L^{-1}$,反应Ⅰ的平衡常数$K=\frac{(0.005 - 0.002)×0.01^{2}}{(0.013 - 0.01)^{2}×(0.013 - 0.01)^{2}}≈3.3×10^{4}$;反应平衡后再加入少量CCl₄充分振荡,I₂进入CCl₄中,反应Ⅱ逆向移动,$c_{平}(I_{2})$减小,$c_{平}(I^{-})$增大,重新平衡后水溶液中$c_{平}(I_{2})·c_{平}(I^{-})$的值变小。
查看更多完整答案,请扫码查看


