2025年金版新学案高中同步导学高中物理必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金版新学案高中同步导学高中物理必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
例 5
如图所示,光滑斜面 $ AE $ 被分成四个相等的部分,一个物体由 $ A $ 点静止释放后做匀加速直线运动,下面结论中正确的是( )
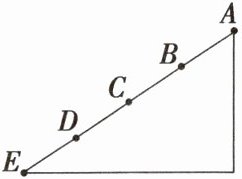
A.经过每一部分时,其速度变化量均相同
B.物体通过 $ AB $、$ BC $、$ CD $、$ DE $ 段所需的时间之比为 $ 1 : \sqrt{2} : \sqrt{3} : 2 $
C.物体到达各点的速度大小之比为 $ 1 : 2 : 3 : 4 $
D.物体在 $ B $ 点的速度大小是在 $ E $ 点速度大小的一半
尝试解题:
如图所示,光滑斜面 $ AE $ 被分成四个相等的部分,一个物体由 $ A $ 点静止释放后做匀加速直线运动,下面结论中正确的是( )

A.经过每一部分时,其速度变化量均相同
B.物体通过 $ AB $、$ BC $、$ CD $、$ DE $ 段所需的时间之比为 $ 1 : \sqrt{2} : \sqrt{3} : 2 $
C.物体到达各点的速度大小之比为 $ 1 : 2 : 3 : 4 $
D.物体在 $ B $ 点的速度大小是在 $ E $ 点速度大小的一半
尝试解题:
答案:
例5 D 根据匀变速直线运动的位移—时间公式$x = \frac{1}{2}at^{2}$,可得$t = \sqrt{\frac{2x}{a}}$,因为$AB$、$AC$、$AD$、$AE$段的位移之比为$1:2:3:4$,则有$t_{B}:t_{C}:t_{D}:t_{E} = 1:\sqrt{2}:\sqrt{3}:2$,可知物体通过$AB$、$BC$、$CD$、$DE$段所需的时间之比为$1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):(2 - \sqrt{3})$,因为通过连续相等位移所用的时间不等,根据$\Delta v = at$可知,经过每一部分的速度变化量不等,故$A$、$B$错误;根据匀变速直线运动的速度—位移公式$v^{2} = 2ax$,可得$v = \sqrt{2ax}$,因为$AB$、$AC$、$AD$、$AE$段的位移之比为$1:2:3:4$,则有$v_{B}:v_{C}:v_{D}:v_{E} = 1:\sqrt{2}:\sqrt{3}:2$,故$C$错误;根据$v_{B}:v_{C}:v_{D}:v_{E} = 1:\sqrt{2}:\sqrt{3}:2$,可知物体在$B$点速度大小是在$E$点速度大小的一半,故$D$正确。故选$D$。
针对练 1.
(2024·浙江丽水期末)如图是无轨小火车,已知小火车由 $ 5 $ 节长度均为 $ 2 \, m $ 的车厢组成,车厢间的空隙不计,小明站在地面上保持静止,且与第一节车厢头部对齐,火车从静止开始启动做 $ a = 0.2 \, m/s^2 $ 的匀加速直线运动,下列说法正确的是( )

A.第 $ 1 $、$ 2 $、$ 3 $ 节车厢经过小明的时间之比是 $ 1 : 2 : 3 $
B.第 $ 1 $、$ 2 $、$ 3 $ 节车厢尾分别经过小明时的速度之比是 $ 1 : 2 : 3 $
C.第 $ 3 $ 节车厢经过小明的时间是 $ 2\sqrt{15} \, s $
D.第 $ 5 $ 节车厢尾经过小明瞬间的速度是 $ 2 \, m/s $
(2024·浙江丽水期末)如图是无轨小火车,已知小火车由 $ 5 $ 节长度均为 $ 2 \, m $ 的车厢组成,车厢间的空隙不计,小明站在地面上保持静止,且与第一节车厢头部对齐,火车从静止开始启动做 $ a = 0.2 \, m/s^2 $ 的匀加速直线运动,下列说法正确的是( )

A.第 $ 1 $、$ 2 $、$ 3 $ 节车厢经过小明的时间之比是 $ 1 : 2 : 3 $
B.第 $ 1 $、$ 2 $、$ 3 $ 节车厢尾分别经过小明时的速度之比是 $ 1 : 2 : 3 $
C.第 $ 3 $ 节车厢经过小明的时间是 $ 2\sqrt{15} \, s $
D.第 $ 5 $ 节车厢尾经过小明瞬间的速度是 $ 2 \, m/s $
答案:
针对练1. D 设每节车厢的长度为$L$,则有$L = \frac{1}{2}at_{1}^{2}$,$2L = \frac{1}{2}at_{2}^{2}$,$3L = \frac{1}{2}at_{3}^{2}$,可得$t_{1}:t_{2}:t_{3} = 1:\sqrt{2}:\sqrt{3}$,则第$1$、$2$、$3$节车厢经过小明的时间之比是$t_{1}:(t_{2}-t_{1}):(t_{3}-t_{2}) = 1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2})$,故$A$错误;第$1$、$2$、$3$节车厢尾经过小明时的速度为$v_{1} = at_{1}$,$v_{2} = at_{2}$,$v_{3} = at_{3}$,则第$1$、$2$、$3$节车厢尾经过小明时的速度之比是$v_{1}:v_{2}:v_{3} = t_{1}:t_{2}:t_{3} = 1:\sqrt{2}:\sqrt{3}$,故$B$错误;第$1$节车厢经过小明的时间是$t_{1} = \sqrt{\frac{2L}{a}} = 2\sqrt{5} s$,则第$3$节车厢经过小明的时间是$t = ( \sqrt{3}-\sqrt{2})t_{1} = 2(\sqrt{15}-\sqrt{10}) s$,故$C$错误;第$1$节车厢尾经过小明瞬间的速度是$v_{1} = at_{1} = 0.4\sqrt{5} m/s$,则第$5$节车厢尾经过小明瞬间的速度是$v_{5} = \sqrt{5}v_{1} = 2 m/s$,故$D$正确。故选$D$。
针对练 2.
(2024·贵州安顺高一上学期期末)如图所示,某列车在一次运行测试中,从 $ a $ 点开始做匀减速直线运动,通过连续四段相等的位移 $ x $,运动到 $ e $ 点时速度减为零,列车可视为质点。下列说法正确的是( )

A.$ ae $ 段的平均速度等于通过 $ c $ 点的瞬时速度
B.$ ac $ 段和 $ ce $ 段所用时间之比为 $ \sqrt{2} : 1 $
C.$ ab $ 段和 $ de $ 段的平均速度大小之比为 $ 1 : (2 - \sqrt{3}) $
D.列车通过 $ a $、$ b $、$ c $、$ d $ 点时的速度大小之比为 $ 4 : 3 : 2 : 1 $
(2024·贵州安顺高一上学期期末)如图所示,某列车在一次运行测试中,从 $ a $ 点开始做匀减速直线运动,通过连续四段相等的位移 $ x $,运动到 $ e $ 点时速度减为零,列车可视为质点。下列说法正确的是( )

A.$ ae $ 段的平均速度等于通过 $ c $ 点的瞬时速度
B.$ ac $ 段和 $ ce $ 段所用时间之比为 $ \sqrt{2} : 1 $
C.$ ab $ 段和 $ de $ 段的平均速度大小之比为 $ 1 : (2 - \sqrt{3}) $
D.列车通过 $ a $、$ b $、$ c $、$ d $ 点时的速度大小之比为 $ 4 : 3 : 2 : 1 $
答案:
针对练2. C $c$点是位移的中点,不是时间的中点,故列车通过$ae$段的平均速度不等于通过$c$点的瞬时速度,故$A$错误;逆向思维,列车反向做匀加速直线运动,根据速度—位移公式$v^{2} = 2ax$,可知,列车通过$a$、$b$、$c$、$d$点时的速度大小之比为$2:\sqrt{3}:\sqrt{2}:1$,故$D$错误;根据匀变速直线运动规律$x = \frac{1}{2}at^{2}$可知,列车通过$ab$段和$de$段的时间之比为$(2 - \sqrt{3}):1$,根据平均速度的公式$\overline{v} = \frac{x}{t}$,可知$ab$段和$de$段的平均速度大小之比为$1:(2 - \sqrt{3})$,故$C$正确;根据匀变速直线运动规律$x = \frac{1}{2}at^{2}$可知,列车通过$ac$段和$ce$段所用时间之比为$[(2 - \sqrt{3}) + (\sqrt{3}-\sqrt{2})]:[(\sqrt{2}-1)+1] = (\sqrt{2}-1):1$,故$B$错误。故选$C$。
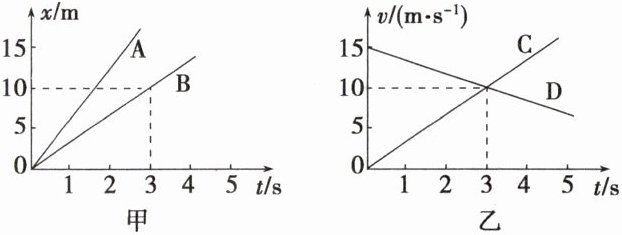
【师生互动】 有四个物体 A、B、C、D,物体 A、B 运动的 $x - t$ 图像如图甲所示;物体 C、D 从同一地点沿同一方向运动的 $v - t$ 图像如图乙所示。完成下列任务:
任务 1. 物体 A 和 B 做匀变速直线运动还是匀速直线运动?
任务 2. 在 $0\sim3\ s$ 的时间内,物体 A、B 的间距逐渐增大还是减小?
任务 3. 在 $0\sim3\ s$ 的时间内,物体 C、D 的间距逐渐增大还是减小?
任务 1. 物体 A 和 B 做匀变速直线运动还是匀速直线运动?
任务 2. 在 $0\sim3\ s$ 的时间内,物体 A、B 的间距逐渐增大还是减小?
任务 3. 在 $0\sim3\ s$ 的时间内,物体 C、D 的间距逐渐增大还是减小?

答案:
任务1.物体A和B均做匀速直线运动。
任务2.增大。
任务3.增大。
任务2.增大。
任务3.增大。
查看更多完整答案,请扫码查看


