《2025年春如金卷课时同步ABC九年级数学上册北师大版》

9. 如图，$E$，$F$ 两点分别在正方形 $ABCD$ 的边 $CD$，$AD$ 上，且 $EF$ 垂直于 $BE$. 若 $AB = 8$，$BE = 10$，则 $\triangle DEF$ 的周长为（ ）

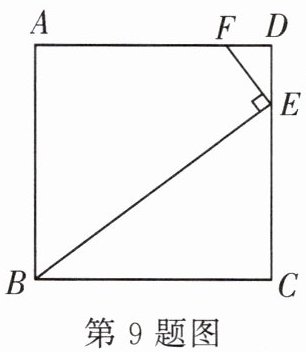
A.$5$
B.$6$
C.$7$
D.$8$

答案： B

10. 如图，已知四边形 $ABCD$ 为正方形，点 $E$ 是边 $AD$ 上一点，连接 $BE$，点 $F$ 在线段 $BE$ 上，且 $CF \perp BE$，垂足为点 $F$，连接 $AF$. 若 $AF = \sqrt{6}$，$BF = \sqrt{2}$ 则 $CF$ =______.

答案： $2+\sqrt{2}$

11. 如图，将正方形 $OACD$ 放在平面直角坐标系中，点 $O$ 是原点，点 $D$ 的坐标为 $(3,4)$，则点 $A$ 的坐标为______.

答案： (-4,3)

12. 如图，在正方形 $ABCD$ 中，点 $E$，$F$ 分别在 $AD$，$CD$ 上，且 $AE = DF$，$BE$ 与 $AF$ 相交于点 $O$，$P$ 是 $BF$ 的中点，连接 $OP$.
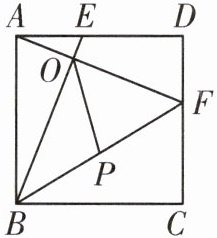
(1) $BE$ 与 $AF$ 之间有怎样的关系？请说明理由；
(2) 若 $AE = DF = 1$，$AB = 4$，求 $OP$ 的长.

答案：
(1) BE=AF且BE⊥AF；
(2) 5/2。

13. 问题引入：如图 1，$AB // CD$，$AB ＞ CD$，$\angle ABD = 90°$，$E$ 是线段 $AC$ 的中点. 连结 $DE$ 并延长交 $AB$ 于点 $F$，连接 $BE$. 则 $BE$ 与 $DE$ 之间的数量关系是______.
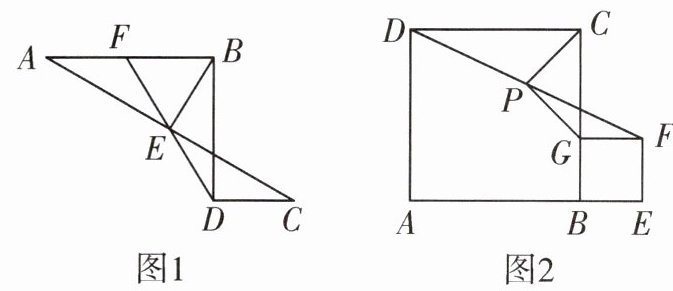
问题延伸：如图 2，在正方形 $ABCD$ 和正方形 $BEFG$ 中，点 $A$，$B$，$E$ 在同一条直线上，点 $G$ 在 $BC$ 上，$P$ 是线段 $DF$ 的中点，连接 $PC$，$PG$.
(1) 判断 $PC$ 与 $PG$ 之间的数量关系，并说明理由；
(2) 连结 $CF$，若 $AB = 3$，$PC = \sqrt{2}$，则 $CF$ 的长为______.

答案： BE=DE；PC=PG；√5