《2025年春如金卷课时同步ABC九年级数学上册北师大版》

7. 如图，在菱形 $ABCD$ 中，对角线 $AC$ 与 $BD$ 交于点 $O$，$OE\perp AB$，垂足为点 $E$。若 $\angle ADC = 128^{\circ}$，则 $\angle AOE$ 的大小为______。

答案： $64^{\circ}$

8. 如图，菱形 $ABCD$ 的周长为 $8$，对角线 $AC$ 和 $BD$ 相交于点 $O$，$AC:BD = 1:2$，则 $AO:BO =$______，菱形 $ABCD$ 的面积 $S =$______。

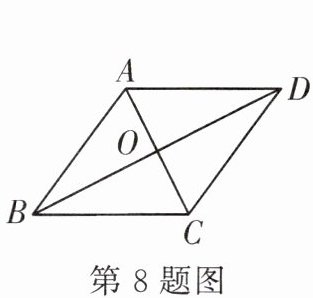
答案： $1:2$，$\frac{16}{5}$

9. 如图，在平面直角坐标系中，菱形 $OABC$ 的顶点 $A$ 的坐标为 $(4,0)$，$\angle AOC = 60^{\circ}$，则顶点 $B$ 的坐标是______。

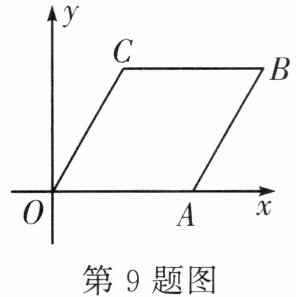
答案： (6, 2√3)

10. 如图，菱形 $ABCD$ 的周长为 $20$，面积为 $24$，点 $P$ 是对角线 $BD$ 上一点，分别作点 $P$ 到直线 $AB$，$AD$ 的垂线段 $PE$，$PF$，则 $PE + PF$ 等于______。

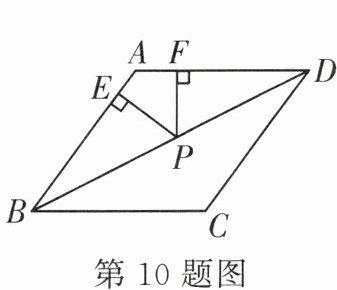
答案： $\frac{24}{5}$

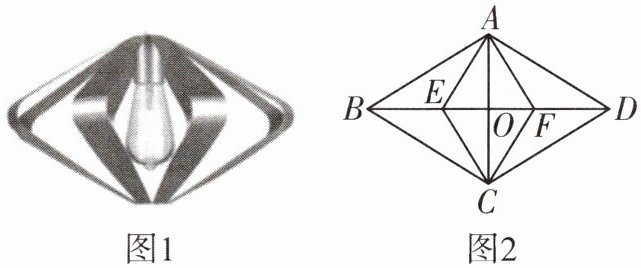
11. 小颖新房买了一盏简单而精致的吊灯（图1），其正面的平面图如图2所示，四边形 $ABCD$ 是一个菱形外框架，对角线 $AC$，$BD$ 相交于点 $O$，四边形 $AECF$ 是其内部框架，且点 $E$、$F$ 在 $BD$ 上，$BE = DF$。
(1) 求证：四边形内部框架 $AECF$ 为菱形；
(2) 若 $AE\perp AD$，$F$ 为 $DE$ 的中点，$AB = 6\sqrt{3}$，求四边形 $AECF$ 的周长。
]

答案：
(1) 见证明过程；
(2) $24$