《2025年春如金卷课时同步ABC九年级数学上册北师大版》

1. 如图，现将一幅长60 cm，宽50 cm的照片贴在一张矩形衬纸的正中央，照片四周外露衬纸的宽度相同，均为x cm，已知矩形衬纸的面积为420 cm²，则下列方程正确的是（ ）


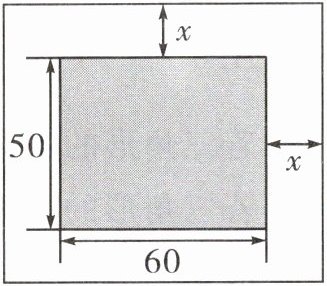
A.$(50 + 2x)(60 + 2x) = 420$
B.$2(50 + 2x)(60 + 2x) = 420$
C.$(50 + x)(60 + x) = 420$
D.$2(50 + x)(60 + x) = 420$

答案： A

2. 为迎接“创文创卫”复检工作，学校准备将一块长30 m、宽20 m的矩形空地进行美化利用，计划在这块地上划出四分之一的区域种花，小红同学设计方案如图，求花带的宽度.若设花带的宽度为x m，则可列方程为（ ）


A.$(30 - x)(20 - x) = \frac{3}{4}×20×30$
B.$(30 - 2x)(20 - x) = \frac{1}{4}×20×30$
C.$30x + 2×20x = \frac{1}{4}×20×30$
D.$(30 - 2x)(20 - x) = \frac{3}{4}×20×30$

答案： D

3. 如图，$AB⊥CB$，$AB = 10$ cm，$BC = 8$ cm. 一只螳螂从点A以2 cm/s的速度向点B爬行，与此同时，一只蝉从点C以1 cm/s的速度向点B爬行，当螳螂和蝉爬行x s后，它们分别到达了M，N两点的位置，此时，$△MNB$的面积恰好为24 cm². 根据题意可列方程为（ ）


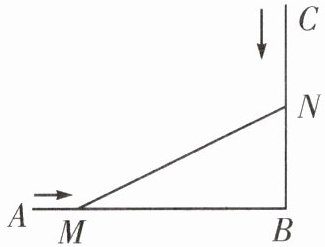
A.$2x·x = 24$
B.$(10 - 2x)(8 - x) = 24$
C.$(10 - x)(8 - 2x) = 24$
D.$(10 - 2x)(8 - x) = 48$

答案： D

4. 如果一个直角三角形的两条直角边长之和为14 cm，面积为24 cm²，那么它的两条直角边的长为________.

答案： 6cm和8cm（或 8cm和6cm，顺序不影响）

5. 若一个直角三角形的斜边长是$2\sqrt{5}$ cm，两条直角边的和为6 cm，则两条直角边的长分别为________.

答案： $2$cm 和 $4$cm（按题目要求此处应直接填数值的话，本题无对应选项格式，以文本形式给出结果）