《2025年春如金卷课时同步ABC九年级数学上册北师大版》

1. 两角对应______的两个三角形相似.

答案： 相等

2. 如图，在△ABC中，点D在AB上(不与A，B两点重合)，连接CD.只需添加一个条件即可证明△ACD与△ABC相似.这个条件可以是______(写出一个即可).

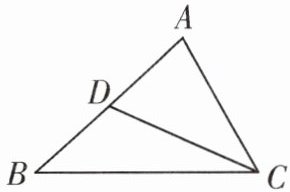
答案： ∠ACD=∠B

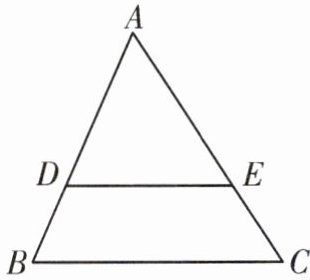
3. 如图，DE//BC，AD=4，BD=2，BC=6.
(1)求证：△ADE∽△ABC；
(2)求DE的长.

答案：
(1)
因为 $DE // BC$，
所以 $\angle ADE = \angle ABC$，$\angle AED = \angle ACB$。
根据相似三角形的判定定理（AA相似），
所以 $\triangle ADE \sim \triangle ABC$。
(2)
由 $\triangle ADE \sim \triangle ABC$，
根据相似三角形的性质，
有 $\frac{AD}{AB} = \frac{DE}{BC}$。
已知 $AD = 4$，$BD = 2$，
所以 $AB = AD + BD = 6$。
已知 $BC = 6$，
代入比例式得 $\frac{4}{6} = \frac{DE}{6}$，
解得 $DE = 4$。

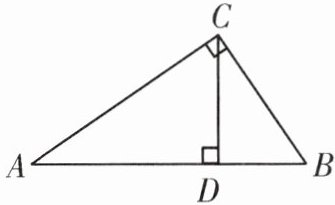
4. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为点D.求证：
(1)AC²=AD·AB；
(2)BC²=BD·AB；
(3)CD²=AD·BD.

答案：
(1) 在$Rt \triangle ABC$和$Rt \triangle ACD$中，
$\because \angle ACB = \angle ADC = 90°$，$\angle A$为公共角，
$\therefore \triangle ABC \sim \triangle ACD$，
$\therefore \frac{AC}{AB} = \frac{AD}{AC}$，
$\therefore AC^2 = AD \cdot AB$。
(2) 在$Rt \triangle ABC$和$Rt \triangle BCD$中，
$\because \angle ACB = \angle BDC = 90°$，$\angle B$为公共角，
$\therefore \triangle ABC \sim \triangle BCD$，
$\therefore \frac{BC}{AB} = \frac{BD}{BC}$，
$\therefore BC^2 = BD \cdot AB$。
(3) 在$Rt \triangle ACD$和$Rt \triangle BCD$中，
$\because \angle ADC = \angle BDC = 90°$，$\angle ACD + \angle BCD = 90°$，$\angle B + \angle BCD = 90°$，
$\therefore \angle ACD = \angle B$，
$\therefore \triangle ACD \sim \triangle BCD$，
$\therefore \frac{CD}{BD} = \frac{AD}{CD}$，
$\therefore CD^2 = AD \cdot BD$。

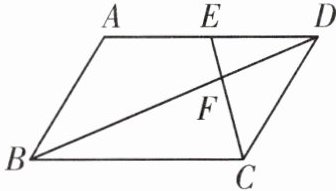
5. 如图，在□ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC=（ ）

A.1：1
B.1：2
C.3：2
D.3：17

答案： B