《2025年春如金卷课时同步ABC九年级数学上册北师大版》

1. 相似三角形______的比、______的比、______的比等于相似比.

答案： 对应高；对应中线；对应角平分线

2. 已知，$\triangle ABC \backsim \triangle DEF$，$\triangle ABC$与$\triangle DEF$的面积之比为$1:2$，当$BC = 1$，对应边$EF$的长是（ ）

A.$\sqrt{2}$
B.$2$
C.$3$
D.$4$

答案： A

3. 若两个相似三角形对应中线的比为$\frac{2}{3}$，则它们对应边上的高之比为（ ）

A.$\frac{4}{9}$
B.$\frac{2}{3}$
C.$\frac{1}{3}$
D.$\frac{\sqrt{6}}{3}$

答案： B

4. 若两个相似三角形的相似比是$7:3$，则这两个三角形对应中线的比是______.

答案： $7:3$

5. 如果两个相似三角形对应角平分线的比是$\sqrt{2}:5$，那么它们对应高的比是______.

答案： $\sqrt{2}:5$

6. 若$\triangle ABC \backsim \triangle A_1B_1C_1$，$AB:A_1B_1 = 3:5$，$BE$，$B_1E_1$分别是它们的对应中线，则$BE:B_1E_1 =$______.

答案： $3:5$

7. 如图，$D$，$E$两点分别是$AC$，$AB$上的点，$\triangle ADE \backsim \triangle ABC$，$DE = 8$，$BC = 24$，$AD = 6$，$\angle B = 70^{\circ}$，求$AB$的长和$\angle ADE$的度数.

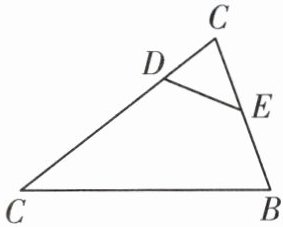
答案： $ \because \triangle ADE \backsim \triangle ABC $,
$ \therefore \frac{DE}{BC} = \frac{AD}{AB} $,
即$ \frac{8}{24} = \frac{6}{AB} $,
解得$AB = 18$。
$ \because \triangle ADE \backsim \triangle ABC $,
$ \therefore \angle ADE = \angle B = 70^{\circ} $。
综上，$AB$的长为$18$，$\angle ADE = 70^{\circ}$。

8. 如图，在矩形$ABCD$中，点$EF$分别在边$AD$，$DC$上，$\triangle ABE \backsim \triangle DEF$，$AB = 6$，$AE = 9$，$DE = 2$.
(1) 求$EF$的长；
(2) 求证：$\angle BEF = 90^{\circ}$.

答案：
(1) √13；
(2) 见解析。

9. 如图，在$\triangle ABC$纸板中，$AC = 4$，$BC = 8$，$AB = 11$，点$P$是$BC$上一点，沿过点$P$的直线剪下一个与$\triangle ABC$相似的小三角形纸板. 针对$CP$的不同取值，两人有如下的说法. 下列判断正确的是（ ）
甲：若$CP = 4$，则有$3$种不同的剪法；
乙：若$CP = 2$，则有$4$种不同的剪法.

A.甲错，乙对
B.甲对，乙错
C.甲和乙都错
D.甲和乙都对

答案： B