《2025年春如金卷课时同步ABC九年级数学上册北师大版》

10. 在如图的正方形网格中，每个小正方形的边长均为$1$，$A$，$B$，$C$，$E$，$F$五点均在格点上. 若$\triangle ABC \backsim \triangle DFE$，则$\triangle DFE$的面积是______.

答案： 2

11. 如图，在$Rt\triangle ABC$中，已知$\angle C = 90^{\circ}$，$BC = 4$，$AC = 8$，点$D$在斜边$AB$上，分别作$DE \perp AC$，$DF \perp BC$，垂足分别为点$E$，$F$，得四边形$DECF$. 设$DE = x$，$DF = y$.
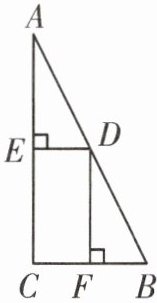
(1) 将$AE$的长用含$y$的代数式表示为$AE =$______；
(2) 写出$y$与$x$之间的函数解析式和$x$的取值范围；
(3) 设四边形$DECF$的面积为$S$，求$S$与$x$之间的函数解析式.

答案：
(1)
因为$DE\perp AC$，$AC = 8$，$DE = x$，$DF = y$，且$DE// BC$（因为$DE\perp AC$，$BC\perp AC$），
根据平行四边形$DECF$的对边相等，$EC = DF = y$，
所以$AE=8 - y$。
(2)
因为$DE// BC$，所以$\triangle AED\sim\triangle ACB$，
则$\frac{AE}{AC}=\frac{DE}{BC}$，
已知$AC = 8$，$BC = 4$，$AE = 8 - y$，$DE = x$，
代入可得$\frac{8 - y}{8}=\frac{x}{4}$，
$8 - y = 2x$，
$y = 8 - 2x$，
因为点$D$在斜边$AB$上，$0\lt x\lt4$。
(3)
$S = xy=x(8 - 2x)=-2x^{2}+8x(0\lt x\lt4)$。
故答案为：
(1)$8 - y$；
(2)$y = 8 - 2x(0\lt x\lt4)$；
(3)$S=-2x^{2}+8x(0\lt x\lt4)$。

12. 有一块锐角三角形余料$ABC$，它的边$BC = 120\ mm$，$BC$边上的高$AD = 80\ mm$.
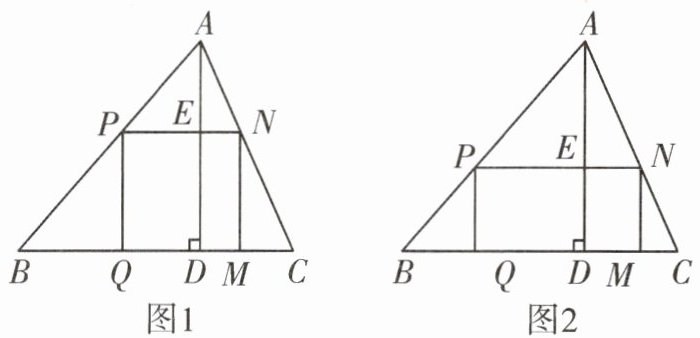
(1) 如图1，把它加工成正方形零件，使正方形的一边在$BC$上，其余两个顶点分别在$AB$，$AC$上. 加工成的正方形零件的边长是多少？
(2) 如图2，把它加工成矩形零件，使矩形的一边在$BC$上，其余两个顶点分别在$AB$，$AC$上. 若这个矩形的边$PN:PQ = 2:1$，则这个矩形的长、宽各是多少？

答案：
(1)设正方形边长为$x\ mm$，则$PN = x$，$AE = 80 - x$。
因为$PN // BC$，所以$\triangle APN \sim \triangle ABC$。
由相似三角形性质得$\frac{AE}{AD}=\frac{PN}{BC}$，即$\frac{80 - x}{80}=\frac{x}{120}$。
解得$x = 48$。
(2)设$PQ = k$，则$PN = 2k$，$AE = 80 - k$。
因为$PN // BC$，所以$\triangle APN \sim \triangle ABC$。
由相似三角形性质得$\frac{AE}{AD}=\frac{PN}{BC}$，即$\frac{80 - k}{80}=\frac{2k}{120}$。
解得$k=\frac{240}{7}$，则$PN = 2k=\frac{480}{7}$。
(1)正方形边长为$48\ mm$；
(2)矩形长为$\frac{480}{7}\ mm$，宽为$\frac{240}{7}\ mm$。