《2025年春如金卷课时同步ABC九年级数学上册北师大版》

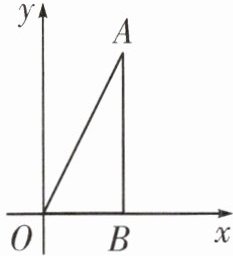
7. 如图，在平面直角坐标系中，$A(2,4)$，$B(2,0)$，将 $\triangle OAB$ 以点 $O$ 为位似中心缩小一半，则点 $A$ 对应的点的坐标为（ ）

A.$(1,2)$或 $(-1,-2)$
B.$(2,1)$或 $(-2,-1)$
C.$(-1,-2)$
D.$(1,2)$

答案： A

8. 如图，已知 $□ ABCD$，以点 $B$ 为位似中心，作 $□ ABCD$ 的位似图形 $□ EBFG$，位似图形与原图形的位似比为 $\frac{2}{3}$，连接 $AG$，$DG$. 若 $□ ABCD$ 的面积为 $24$，则 $\triangle ADG$ 的面积为__________.

答案： 4

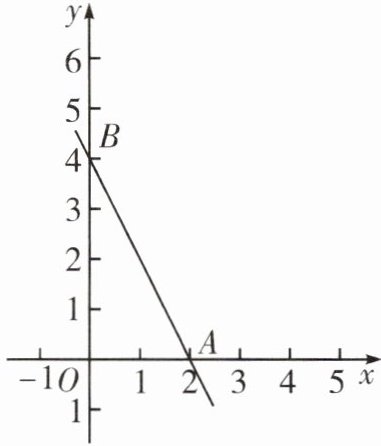
9. 如果两个一次函数 $y = k_1x + b_1$ 和 $y = k_2x + b_2$ 满足 $k_1 = k_2$，$b_1 \neq b_2$，那么称这两个一次函数为“平行一次函数”. 如图，已知函数 $y = -2x + 4$ 的图象与 $x$ 轴、$y$ 轴分别交于 $A$，$B$ 两点，一次函数 $y = kx + b$ 与 $y = -2x + 4$ 是“平行一次函数”.
(1) 若函数 $y = kx + b$ 的图象过点 $(1,1)$，求实数 $b$ 的值；
(2) 若函数 $y = kx + b$ 的图象与两坐标轴围成的三角形和 $\triangle AOB$ 构成位似图形，位似中心为原点，位似比为 $1:2$，求函数 $y = kx + b$ 的解析式.

答案：
(1) 由于 $y = kx + b$ 与 $y = -2x + 4$ 是平行一次函数，
$\therefore k = -2$，
把点 $(1,1)$ 代入 $y = -2x + b$，
得$1 = -2 × 1 + b$，
$b = 3$。
(2) 函数 $y = -2x + 4$ 的图象与 $x$ 轴、$y$ 轴分别交于 $A$，$B$ 两点，
由 $y = -2x + 4$，
令$x = 0$，得$y = 4$，
$\therefore B(0,4)$，
令$y = 0$，得$x = 2$，
$\therefore A(2,0)$，
根据位似中心为原点，位似比为 $1:2$，
则 $y = kx + b$ 的图象有两种情况：
不翻折时，函数的图象过 $(\frac{1}{2}×2,0)$ 和 $(0,\frac{1}{2}× 4)$，
即过$(1,0)$，$(0,2)$，
代入$y = -2x + b$，
得$b = 2$，
此时函数为$y = -2x + 2$；
翻折时，函数的图象过 $(-1,0)$，$(0,-2)$，
代入$y = -2x + b$，
得$b = -2$，
此时函数为$y = -2x - 2$。
综上，函数的解析式为：$y = -2x + 2$ 或 $y = -2x - 2$。